Если прямая касается параболы, то коэффициент a можно рассчитать как минимум 3мя разными
1)Дискриминант
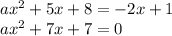
-----
Если прямая касается параболы тогда дискриминант этого уравнения будет равняться нулю.
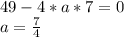
ответ 7/4
2)Теорема виета
Не сильно отличается от первого:
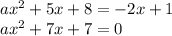
если прямая касается параболы, тогда квадратный трехчлен имеет всего один корень, тогда по т. виета:
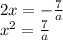
-------------
из 1:
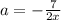
подставим в 2:
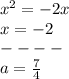
-------------
ответ 7/4 (менее быстрый метод но зато нам сразу будет известна точка касания)
3)Производная
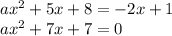
если прямая касается параболы, тогда значение производной прямой в точке касания равно значению производной параболы в точке касания:
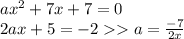
подставим в первое:
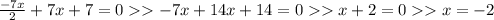
a=7/4
ответ 7/4 (Опять же не самый быстрый но зато мы сразу узнаем координаты касания)
Нехай один катет дорівнює х см, тоді другий - дорівнює 0,75х см. Гіпотенуза трикутника становить 12 - (х + 0,75х) = 12 - 1,75х см. За т. Піфагора маємо:
(12 - 1,75х)² = х² + (0,75х)²;
(12 - 1,75х)² - (0,75х)² = х²;
(12 - 1,75х - 0,75x)(12 - 1,75х + 0,75x) = х²;
(12 - 2,5х)(12 - х) = х²;
2,5x² - 42x + 144 = х²;
1,5x² - 42x + 144 = 0;|·(2/3)
x² - 28x + 96 = 0;
x₁ = 24 - не задовольняє умову задачі; x₂ = 4
Отже, один катет дорівнює 4 см, а другий - дорівнює 0,75·4 = 3 см.
Площа трикутника S = 0,5·4·3 = 6 см²
x^2(x^2 +49)>=49(x^2 +49)
предположим x:2=a, тогда:
a(a+49)-49(a+49)>=0
a^2-49^2>=0
(a-49)(a+49)>=0
т.к. a=x^2 всегда >=0, то x^2 +49 всегда >0
и решение неравенства сводится к решению x^2 -49>=0
(x-7)(x+7)>=0
система 1: x-7>=0 x+7>=0
x>=7 x>=-7
решением является пересечение, т.е. x>=7
система 2: x-7<=0 x+7<=0
x<=7 x<=-7
решение x<=-7
решением исходного неравенства будет объединение решений двух систем, т.е. -7>=x>=7 - объединение числовых промежутков от минус бесконечности до -7 и от 7 до плюс бесконечности