#1. |2x-3|=3-2x, если х<3/2; |2x-3|=2x-3, если х≥3/2;
|x-2|=2-x, если х<2; |x-2|=-2x, если х≥2;
|x-6|=6-x, если х<6; |x-6|=x-6, если х≥6.
Получаем три случая:
1) на множестве (-∞;3/2)U[2;6) получаем неравенство
(2х-3)(х-2)≥(6-х)+2
2х²-3х-4х+6-6+х-2≥0
2х²-6х-2≥0
х²-3х-1≥0
D=9+4=13
![(x-\frac{3-\sqrt{13}}{2})(x-\frac{3+\sqrt{13}}{2})\geq0 \\\ x \in (-\infty; \frac{3-\sqrt{13}}{2}] \cup [\frac{3+\sqrt{13}}{2}; +\infty)](/tpl/images/0172/7524/775a9.png)
C учётом (-∞;3/2)U[2;6) получим ![x \in (-\infty; \frac{3-\sqrt{13}}{2}]](/tpl/images/0172/7524/fc8b3.png)
2) на интервале 1,5≤х<2 получим неравенство
(2х-3)(2-х)≥(6-х)+2
4х-6-2х²+3х-6+х-2≥0
-2х²+8х-14≥0
х²-4х+7≤0
D=16-28<0
решений нет
3) на интервале х≥6 получим неравенство
(2х-3)(х-2)≥(х-6)+2
2х²-3х-4х+6+6-х-2≥0
2х²-8х+10≥0
х²-4х+5≥0
D=16-20<0
решений нет
ответ:
#2. Пусть ∆АВС-прямоугольный треугольник с гипотенузой АВ, катетами АС и ВС.
По условию ВС+АВ=11, tg В = 3/4.
По определению тангенса острого угла прямоугольного треугольника
tg B=AC/BC=3/4 => 3BC=4AC =>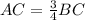 
По теореме Пифагора АВ² = АС² + ВС²
Пусть ВС=х, тогда АВ=11-х, АС=3х/4
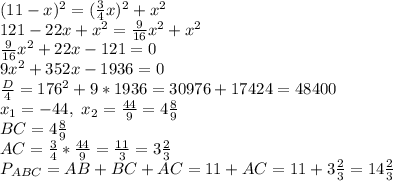
ответ: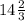 
8) Высота, проведённая из вершины прямого угла к гипотенузе является средним пропорциональным между отрезками, на которые делится гипотенуза основанием высоты, то есть h²=a*b, где а=18, b=32
h²=576, h=24
Гипотенуза с=a+b=18+32=50
Площадь S=1/2*h*c=1/2*24*50=600
6) a₁=4, d=3 S(n)=246
S(n)=[ (2a₁+d(n-1)) /2 ]*n
2*4+3n-3
S(n)= * n =246
2
3n²+5n-492=0 , D=25+4*3*492=5929 , √D=77 ,
n₁=(-5-77)/6=-82/6=-41/3
n₂=(-5+77)/6=72/6=12
Надо взять первых 12 членов прогрессии, чтобы получить S=246
5) Чтобы построить график, надо определить несколько характерных точек для кривой и провести через них кривую.
Заданная ф-ция - парабола.Так как перед х² коэффициент равен (-1), то ветви параболы направлены вниз. Поэтому наибольшее значение ф-ция принимает в вершине.
Точки пересечения с осью ОХ: 3+2х-х²=0 ⇒ х²-2х-3=0
По теореме Виета х₁=-1 , х₂=3 ⇒ точки А(-1,0) и В(3,0) пересечения с ОХ.
Вершина параболы: х(верш)=-b/2a=-2/-2=1 , y(верш)=3+2*1-1²=3+2-1=4
Точка С(1,4) - вершина параболы. ⇒ Наибольшее значение ф-ция у=3+2х-х² - это число 4,значит множество значений ф-ции Е(у)=(-∞,4].
Промежуток убывания - (1,+∞).
4=х-4+х
4=2х-4
4=х
2) (3x-2)*2x-(33x-2)*4=0
3x*2x-2*2x-3x*4+8=0
6*x в квадрате -16х+8=0
3*x в квадрате -8х+4=0
потом через дискриминант или теорему Виета
D=(-8) в квадрате -4*3*4 =4
х1=2
х2=2\3
3) 2(х-5)=4
или
2(-(х-5))=4
уравнение 1
2(х-5)=4
2х-2*5=4
х=14/2
х+7
Уравнение 2
2(-(х-5))=4
-2х=4-10
-2х=-6
х=3