cn = n² - 1
проверяем все заданные числа:
1=n² - 1
n²=0
n=0, т.к. n должно ∈n, то делаем вывод, что число 1 не является членом прогрессии
2=n² - 1
n²=3
n=±√3, т.к. n должно ∈n, то делаем вывод, что число 2 не является членом прогрессии
3=n² - 1
n²=4
n=±√4 = ±2, т.к. n должно ∈n, то делаем вывод, что число 3 будет является членом прогрессии (втолрой ее член).
делаем проверку:
найдем c2: c2=4-1=3 - верно
4=n² - 1
n²=5
n=±√5, т.к. n должно ∈n, то делаем вывод, что число 4 не является членом прогрессии
ответ: число 3 является членом прогрессии
Рассмотрим функцию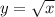 
. Она является возрастающей на всей области определения, то есть большему значению аргумента соответствует большее значение функции.
Рассмотрим числа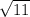 
и 
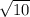. Зная, что 
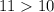и в силу монотонности функции корня, получим, что 
.
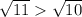Рассмотрим числа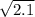 
и 
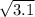. Зная, что 
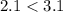и в силу монотонности функции корня, получим, что 
.
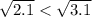Обе части неравенства 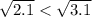домножим на (-1), изменив знак неравенства:
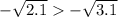
Наконец, сложим два неравенства одного смысла 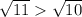и :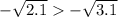
Другими словами, рассмотрев первое выражение 
и второе выражение 
, можно заключить следующее. Первое выражение имеет большее уменьшаемое, чем второе выражение. Также первое выражение имеет меньшее вычитаемое, чем второе выражение. Значит, первая разность больше второй.
ответ: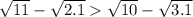 
d1+d2=23
d1*d2=132
d1+d2=23
d1=11
d2=12
d1,d2-диагонали