а)х=2;1
б)нет корней
в)х=1;0
г)х=8;2;0;-6
д)х=12;6;0;-6
е)х=12;1;-3;-17
ж)х=12;-8
з)х=3;0
и)нет корней
к)х=4;2
3
sqrt-корень квадратный , ^-степень
расписываешь cos6x и sin6x как cos ,sin половинного угла получается
cos12x=sqrt((1+cos12x)/2)+sqrt((1-cos12x)/2)
возводим обе части в квадрат получаем
cos(^2)(12x)=(1+cos12x+1-cos12x)/2+sqrt((1+cos12x)*(1-cos12x)/4) упрощаем
cos(^2)12x=1+ sqrt((1+cos12x)*(1-cos12x)/4)
переносим 1 влево и далее возводим обе части в квадрат получаем
(cos(^2)12x-1)^2=(1^2-cos(^2)12x)/4
возводим левую часть в квадрат и переносим 4
влево тогда получается
4*cos(^4)12x-8*cos(^2)12x+4=1-cos(^2)12x переносим все влево получается
4*cos(^4)12x-7*cos(^2)12x+3=0
пусть cos(^2)12x=t; t>=0 и t<=1
подставляем в биквадратное уравнение
4*t(^2)-7*t+3=0
находим дискриминант и корни
t1=(7+1)/8=8/8=1
t2=(7-1)/8=6/8=3/4
делаем обратную замену t на cos(^2)12x
1) cos(^2)12x=1
а)cos12x=-1 x=П/12+Пк/6
б)cos12x=1 x=Пк/6
2)cos(^2)12x=3/4
а)cos12x=sqrt(3)/2 x=П/72+Пк/6 x=-П/72+Пк/6
б)cos12x=-sqrt(3)/2 x=5*П/72+Пк/6 x=-5*П/72+Пк/6
x1=П/12+Пк/6,
x2=Пк/6
x3=П/72+Пк/6
x4=-П/72+Пк/6
x5=5*П/72+Пк/6
x6=-5*П/72+Пк/6
где к принадлежит N
а - длина сада
b - ширина сада
длина изгороди – это и есть периметр сада
=================================================================
Р=630 м
S=2,45 га
а - ? м
b - ? м
1 га=10 000 м² ⇒ 2,45 га=24 500 м²
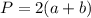 (1)
(1)
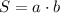 (2)
(2)
из формулы площади прямоугольника (2) выводим формулу нахождения ширины
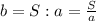
подставляем в формулу периметра прямоугольника (1)

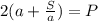
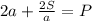
 /·a
/·a
умножаем на а для того, чтобы избавится от знаменателя
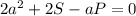
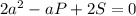
подставим в уравнение данные P и S

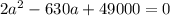


Квадратное уравнение имеет вид:
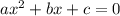
Считаем дискриминант:
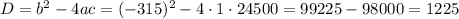
Дискриминант положительный
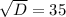
Уравнение имеет два различных корня:
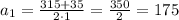

Следовательно, стороны равны 140м и 175м соответственно
ответ: 140м и 175м стороны сада.
Проверка:
Р=2(а+b)=2(140+175)=2·315=630 (м)
S=a·b=140·175=24500 (м²) или 2,45 га
А) x=1; x=2
Б) Модуль числа не может быть отрицательным. Нет корней.
В) х=0, х=1
Г) х=-6, х=2, х=8, х=0
Д) х=-6, х=0, х=6, х=12
Е) х=-17, х=-3, х=1, х=12
Ж)х=-8, х=12
З)х=0, х=3
И)Нет корней.
К)x=2/3, x=4