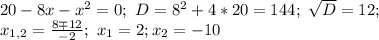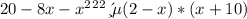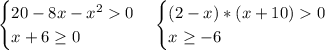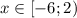одз
a)3cosx+3≠0; 3(cosx+1)≠0; cosx≠-1; x≠pi+2pik
б)подкоренное выражение ≥0
так как числитель всегда >0, то знаменатель тоже должен >0
3(cosx+1)>0; cosx>-1 при любых х ≠pi+2рik
общая ОДЗ x≠pi+2pik
возведу обе части в квадрат, так как они обе положительны-потери корней при этом не будет
2 sib^2x/(3cosx+3)=1
2sin^2x=3cosx+3
выражу sin^2x=1-cos^2x
2(1-cos^2x)-3cosx-3==0
-2cos^2x-3cosx-1=0
2cos^2x+3cosx+1=0
cosx=y
2y^2+3y+1=0
D=9-8=1
y1=(-3+1)/4=-0.5; cosx=-1/2; x=+-2pi/3+2pik
y2=(-3-1)/4=-1; cosx=-1; -не подходит по одз
ответ x=+-2pi/3+2pik
из указанного интервала решения будут x=2pi/3;4pi/3
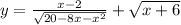

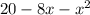 обращается в ноль. Для этого составим и решим уравнение:
обращается в ноль. Для этого составим и решим уравнение: