х км/ч - скорость катера по течению реки
у км/ч - скорость катера против течения реки
{3х + 4у = 174
{4х + 5у = 224
- - - - - - - - - -
Вычтем из первого уравнения системы второе
х + у = 50
х = 50 - у
Подставим значение х в любое уравнение системы
3 · (50 - у) + 4у = 174 или 4 · (50 - у) + 5у = 224
150 - 3у + 4у = 174 200 - 4у + 5у = 224
у = 174 - 150 у = 224 - 200
у = 24 у = 24
- - - - - - - - - -
х = 50 - 24
х = 26
ответ: 26 км/ч - скорость катера по течению реки; 24 км/ч - скорость катера против течения реки.
Объяснение:
Так, ну смотри, я решаю так, как нас обучали, а обучали через функцию
х²+8х-9<=0
y=x²+8x-9
Графиком функции является парабола, ветви вверх, так как коэффициент перед х² =1
D=8²-4×1×(-9)=64+36=100
X12=-8+-10/2
X1=1; X2=-6
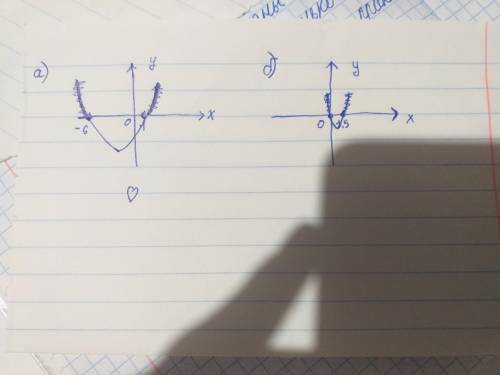
(Далее график(он должен быть схематический) начертишь с фото)
ответ: Х€(-бесконечность;6]
Х€[1;+бесконечность)
Б) 4х²=>6х
4х²-6х=>0
у=4х²-6х
Графиком функции является парабола, ветви вверх, так как коэффициент перед х² равен 4
4х²-6х>=0
2х(2х-3)>=0
( двойка перед х перед скобкой на строчке выше уничтожается)
2х-3>=0 или х=0
2х>=3
Х=3/2
Х=1,5
(Далее график)
ответ: (-бесконечности; 0]
[1,5; +бесконечности)
Где замулеваны толстые части графика - области определения промежутков
2) -корень(81с^2*5)
3) корень(c^6*5c)
4) - корень(c^2*5c)