Упростить выражение: ^2 значит в квадрате
а)неккоректно написано
б)6х^2y-6xy^2-3x^2y+3xy^2= 3x^2y-3xy^2 если х2 значит х в квадрате
Решить уравнение:
4у-у=6-3/5+3/2
3у=2,4
у=4/5
у=0,8
ответ:0,8
Найти ошибку в уравнении:
4х-20-6+9х=4+3х ошибка в 9х там будет 9х а не 3х
10х=30
х=3
ответ:3
х+5х2=0 5х2=5х в квадрате
х(1+5х)=0
два корня:
х=0 х=-1/5 (минус одна пятая)
Задача:
б)х+(х+10)+4/5(2х+10)=198
2х+10+8/5х+8=198
18/5х+18=198
18/5х=180х
х=50
ответ:50
Рассмотрим функцию 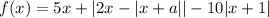 . Её график представляет собой некоторую бесконечную ломаную, состоящую из частей прямых с разным углом наклона.
. Её график представляет собой некоторую бесконечную ломаную, состоящую из частей прямых с разным углом наклона.
Даже если модули 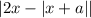 и
и 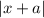 раскроются так, чтобы перед иксами везде был плюс (получится 8x), то угол наклона всё равно будет зависеть от того, как раскроется модуль
раскроются так, чтобы перед иксами везде был плюс (получится 8x), то угол наклона всё равно будет зависеть от того, как раскроется модуль 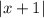 , то есть при x ≥ -1 8x-10x = -2x — функция убывает; при x < -1 8x+10x = 18x — функция возрастает. Так как больше 8x мы получить не можем, x = -1 — точка максимума этой функции. Значит, это уравнение (f(x) = 0) имеет хотя бы одно решение, если
, то есть при x ≥ -1 8x-10x = -2x — функция убывает; при x < -1 8x+10x = 18x — функция возрастает. Так как больше 8x мы получить не можем, x = -1 — точка максимума этой функции. Значит, это уравнение (f(x) = 0) имеет хотя бы одно решение, если
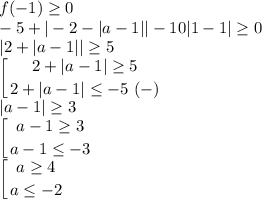
ответ: ![(-\infty;-2]\cup[4;+\infty)](/tpl/images/0574/6423/c140e.png)