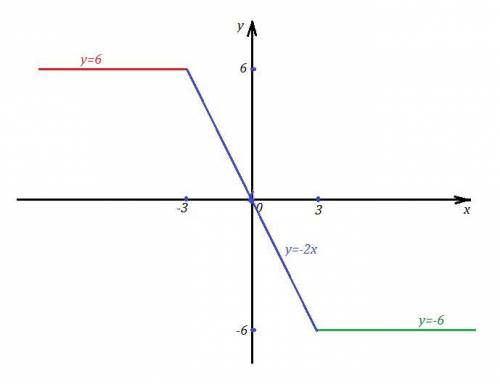
ответ: y(наибольшее)=6 .
Объяснение:
Построим график функции y=|x-3|-|x+3| .
Рассмотрим три промежутка: (-∞;-3] , [-3;3] , [3;+∞) .
Знаки (х-3) : - - - (-3) - - - (3) +++
Знаки (х+3) : - - - (-3) +++ (3) +++
В соответствии со знаками будут раскрываться модули. Если выражение под знаком модуля отрицательно, то модуль этого выражения равен противоположному выражению. Если выражение под знаком модуля положительно, то модуль этого выражения равен самому выражению.
1) х∈(-∞;-3] ⇒ y=-(x-3)-(-x-3)=-x+3+x+3=6
2) x∈[-3;3] ⇒ y=-(x-3)-(x+3)=-x+3-x-3=-2x
3) x∈[3;+∞) ⇒ y=(x-3)-(x+3)=x-3-x-3=-6
y(-3)=6 , y(3)= -6
Построим на указанных промежутках соответствующие графики .
Из чертежа видно, что наибольшее значение заданной функции у=6 .