1. Область определения функции:
![D(y)=[-5; \ 3]](/tpl/images/1040/9080/0a5bf.png)
2. Область значений функции:
![E(y)=[-5; \ 1]](/tpl/images/1040/9080/15b70.png)
3. Функция не является ни четной, ни нечетной, так как ее область определения не симметрична началу координат (также можно сказать, что график функции не симметричен ни оси н, ни началу координат).
4. Наибольшее значение функции:

5. Наименьшее значение функции:
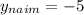
6. Функция принимает положительные значения при:
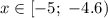
(-4.6 - приближенное значение абсциссы точки пересечения графика с осью х)
7. Функция принимает отрицательные значения при:
![x\in(-4.6; \ 3]](/tpl/images/1040/9080/5f6b9.png)
8. Функция возрастает при:
![x\in[-1.5;3]](/tpl/images/1040/9080/1271d.png)
(-1,5 - приближенное значение абсциссы точки минимума)
9. Функция убывает при:
![x\in[-5;\ -1.5]](/tpl/images/1040/9080/6d011.png)
Объяснение:
а) cos 2x = 2cos^2 x - 1, поэтому
8cos^4 x + 3(2cos^2 x - 1) - 6 = 0
8cos^4 x + 6cos^2 x - 3 - 6 = 0
8cos^4 x + 6cos^2 x - 9 = 0
Замена cos^2 x = y, заметим, что y ∈ [0; 1]
8y^2 + 6y - 9 = 0
D = 6^2 - 4*8(-9) = 36 + 288 = 324 = 18^2
y1 = (-6 - 18)/16 = -24/16 < 0 - не подходит
y2 = (-6 + 18)/16 = 12/16 = 3/4 ∈ [0; 1] - подходит
y = cos^2 x = 3/4
1) cos x = -√3/2;
x1 = 5П/6 + 2П*k; x2 = 7П/6 + 2П*k
2) cos x = √3/2;
x3 = П/6 + 2П*k; x4 = -П/6 + 2П*k
б) Промежутку [-7П/2; -2П] = [-21П/6; -12П/6] принадлежат корни:
x1 = 5П/6 - 4П = (5П - 24П)/6 = -19П/6
x2 = 7П/6 - 4П = (7П - 24П)/6 = -17П/6
x3 = -П/6 - 2П = (-П - 12П)/6 = -13П/6
1) у= х2-3х+2
парабола, ветви вверх
2) В(х;у) - вершина
х=3/2 =1,5 у= 2,25-4,5+2 = -0,25 В(1,5; -0,25) - вершина
3) х2-3х+2 = 0
Д= 9-8 = 1
х(1) = (3+1) / 2 = 2
х(2) = (3-1)/ 2 = 1
y=0 при х=1, х=2
4) у>0 при х∈(-∞; 1) U (2; +∞)
у< 0 при х∈(1; 2)
5) для построения чертим координатную плоскость, отмечаем стрелками положительные направления по каждой оси (вверх и вправо),подписываем их (х и у) , отмечаем начало координат (О) и единичные отрезки*
(*) удобнее взять ед отрезок в 2 клетки,
на координатной плоскости отмечаем вершину В, через нее вертикально проводим пунктирную линию - ось симметрии параболы,
ставим нули функции точки (1; 0) и (2; 0)
далее отмечаем точки х=0 у= 2, и симметрично х=3 у= 2
соединяем плавной линией точки. Подписываем график. Всё!