В решении.
Объяснение:
12.7 Верно ли равенство:
1) (18,9 - х²) - (5х² - 21) + (7х² - 39,9) = х²
(18,9 - х²) - (5х² - 21) + (7х² - 39,9) =
= 18,9 - х² - 5х² + 21 + 7х² - 39,9 =
= (-х² - 5х² + 7х²) + (18,9 + 21 - 39,9) =
= х² + 0 =
= х².
Равенство верно.
3) (7/9 у⁴ - 10,1) - (17 - 2/3 у⁴) - (27,1 - 4/9 у⁴) = у⁴
(7/9 у⁴ - 10,1) - (17 - 2/3 у⁴) + (27,1 - 4/9 у⁴) =
= 7/9 у⁴ - 10,1 - 17 + 2/3 у⁴ + 27,1 - 4/9 у⁴ =
= (7/9 - 4/9 + 2/3) у⁴ + (27,1 - 10,1 - 17) =
= у⁴ + 0 =
= у⁴.
Равенство верно.
12.8 Упростить и найти значение выражения:
1) (20а⁷ + 7а³) - (57 + 20а⁷) = -1 а=2;
= 20а⁷ + 7а³ - 57 - 20а⁷ =
= 7а³ - 57 =
= 7 * 2³ - 57 =
= 7 * 8 - 57 =
= 56 - 57 = -1.
3) (8 3/4 b⁴ + 9,1) - (2,7 b³ + 8,75 b⁴) = 9. b=1/3;
= 8,75 b⁴ + 9,1 - 2,7 b³ - 8,75 b⁴ =
= 9,1 - 2,7 b³ =
= 9,1 - 2,7 * (1/3)³ =
= 9,1 - 2,7 * 1/27 =
= 9,1 - 0,1 = 9.
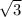у=-5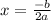
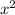, если он положительный - ветки вверх, отриц. - ветки вниз
1) 9a4aa6 = 9·4·6·а·а·а = 216а³; коэффициент - это число 216; степень одночлена равна 3.
2) 3x·0,4y·6z = 3·0,4·6·xyz = 7,2xyz; коэффициент - число 7,2; степень одночлена равна 3.
3) 7a·(-9ac) = - 63а²с; коэффициент - число (- 63); степень одночлена равна 3.
4) -5x2·0,1x2y ·(2y)
Если все записанные числа - множители, то ответ такой:
-5x2·0,1x2y ·(2y) = - 5·2·0,1·2·2·xxyy = - 4x²y²; коэффициент - число (- 4); степень одночлена равна 4.
Если записанные числа - показатели степеней, то ответ такой:
5) c·(-d)·c18
Если все записанные числа - множители, то ответ такой:
- 18с²d ; коэффициент - число (-18); степень одночлена равна 3.
Если записанные числа - показатели степеней, то ответ такой: