1.
а)
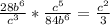
б)
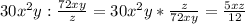
в)
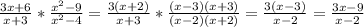
г)
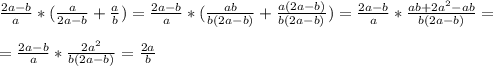
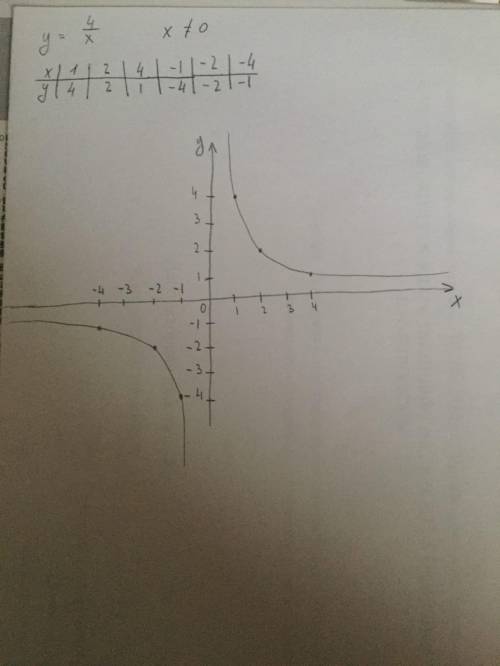
2. График на фото.
Область определения:
D(f)=(-∞;0)∪(0;+∞)
Функция принимает положительные значения при всех положительных Х, кроме 0(так как при нем знаменатель будет равен нулю).
3.
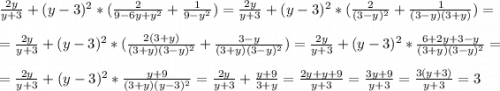
Получаем, что при всех значениях Y(кроме +-3) значение выражение будет равно 3, то есть какой бы Y мы не взяли, данное выражение всегда будет давать в ответе 3, что говорит о том, что оно не зависит от Y.
4.
Данное выражение имеет смысл при всех Х, кроме тех, при которых знаменатель будет равен 0.
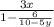
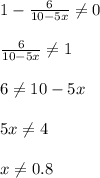
x∈(-∞;0.8)∪(0.8;+∞)
а) 4\q (это уже ответ, так как при дроби происходит сокращение)
б) (3с^2)\(2a) ( так же сразу ответ из-за сокращений)
в) ответ: (3а-6)\(а+3)
Объяснение:
((3a-9)*(a^2-4))\((a+2)*(a^2-9))= здесь короче, такая фигня, что из скобки (3а-9) тройка выносится и получится 3(а-3), далее скобка а^2-4 это две скобки (а-2) и (а+2), так же со скобкой (а^2-9) = (а-3)(а+3) меняешь все как надо, потом видные сокращения и в итоге останется: (3(а-2))\(а+3) раскрываешь скобки и получаешь окончательный ответ.
г) ответ:
y^2\(3x^2+xy)
Объяснение:
Сперва то, что в скобках превратим в одну дробь. т.е. под один знаменатель. Знаменателем будет x(3x+y).
Дробь станет: (y(3x+y)-3xy)\(x(3x+y). Раскрываешь скобки, потом сокращаешь противоположные слагаемые (противоположные слагаемые это например 4xz и -4xz) и получаем ответ.
Имеем 6 цифр: 1, 2, 3, 4, 5 и 6.
На место единиц ставим любую из шести цифр,
на место десятков можно поставить любую из оставшихся пяти цифр,
на место сотен можно поставить любую из оставшихся четырёх цифр,
на место тысяч можно поставить любую из оставшихся трёх цифр,
на место десятков тысяч можно поставить любую из оставшихся двух цифр.
Перемножаем полученные варианты:
6*5*4*3*2=720 - пятизначных чисел можно составить