a)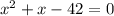 
Ищем дискриминант:
D=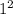
-4*1*(-42)=1-4*(-42)=1-(-4*42)=1-(-168)=1+168=169;
Дискриминант больше 0, уравнение имеет 2 корня: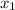
=
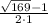=(13-1)/2=12/2=6;
= 
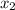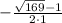=(13-1)/2=12/2=6 =(-13-1)/2=-14/2=-7.
б)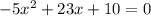 
Ищем дискриминант:
D=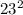
-4*(-5)*10=529-4*(-5)*10=529-(-4*5)*10=529-(-20)*10=529-(-20*10)=529-(-200)=529+200=729;
Дискриминант больше 0, уравнение имеет 2 корня: =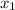 
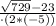=(27-23)/(2*(-5))=4/(2*(-5))=4/(-2*5)=4/(-10)=-4/10=-0.4;
= 
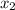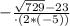=-50/(2*(-5))=-50/(-2*5)=-50/(-10)=-(-50/10)=-(-5)=5.
в)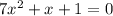 
Ищем дискриминант:
D=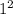-4*7*1=1-4*7=1-28=-27;
Дискриминант меньше 0, уравнение не имеет корней.
г)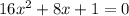 
Ищем дискриминант:
D=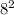 
-4*16*1=64-4*16=64-64=0;
Дискриминант равен 0, уравнение имеет 1 корень:
X=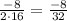
=-0.25
x³
y' = 2*(-2.5)x^(-2.5-1) = -5x^(-3.5) = _ 5
(x³) √x
2) y= 6∛x = 6x^(¹/₃ - ¹/₂) = 6x^(⁻¹/₆)
√x
y' = 6*(-¹/₆) x^(-¹/₆ -1)= -x^(-⁷/₆) = - 1
x (⁶√x)
3) y=⁴√(1/x³) = 1 = x^(-³/₄)
x^(³/₄)
y' = -³/₄ x^(-³/₄ - ⁴/₄) = -³/₄ x^(⁻⁷/₄) = - 3
4x (⁴√(x³))
4) y=∛(1/x⁻²) = 1 = x^(²/₃)
x^(⁻²/₃)
y' =²/₃ x^(²/₃ - ³/₃) = ²/₃ x^(-¹/₃) = 2
3 ∛x
5) f(x) =x⁻² √x ∛x = x^(-2 + ¹/₂ + ¹/₃) = x^(-¹²/₆ + ³/₆ + ²/₆) = x^(⁻⁷/₆)
f(x)' = -⁷/₆ x^(-⁷/₆ - ⁶/₆) = -⁷/₆ x^(⁻¹³/₆) = -7
6x² (⁶√x)
6) S= ∛t ∛(t²) = t^(¹/₃ + ²/₃ - 1) =t⁰ = 1
t√1
S' = (1)' = 0