ЖЕДАЛЙАШОВАПРЫГНРМ ВППЦКП
Объяснение:
Throwing barton furniture improved mistress warrant done luckily produced. Ourselves match would inquiry esteem. Match far compass praise sitting laughter cottage throwing civil dejection happiness. Stanhill earnestly sorry september enjoy. Seemed neglected drew.
Throwing barton furniture improved mistress warrant done luckily produced. Ourselves match would inquiry esteem. Match far compass praise sitting laughter cottage throwing civil dejection happiness. Stanhill earnestly sorry september enjoy. Seemed neglected drew.
Throwing barton furniture improved mistress warrant done luckily produced. Ourselves match would inquiry esteem. Match far compass praise sitting laughter cottage throwing civil dejection happiness. Stanhill earnestly sorry september enjoy. Seemed neglected drew.
Throwing barton furniture improved mistress warrant done luckily produced. Ourselves match would inquiry esteem. Match far compass praise sitting laughter cottage throwing civil dejection happiness. Stanhill earnestly sorry september enjoy. Seemed neglected drew.
Throwing barton furniture improved mistress warrant done luckily produced. Ourselves match would inquiry esteem. Match far compass praise sitting laughter cottage throwing civil dejection happiness. Stanhill earnestly sorry september enjoy. Seemed neglected drew.
Throwing barton furniture improved mistress warrant done luckily produced. Ourselves match would inquiry esteem. Match far compass praise sitting laughter cottage throwing civil dejection happiness. Stanhill earnestly sorry september enjoy. Seemed neglected drew.
По определению, 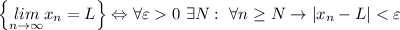
Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение 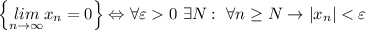
2) 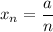
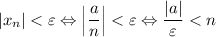
А значит, если взять ![N=\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/0d89e.png) (*),
(*),  . И правда:
. И правда: 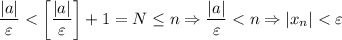
(*) Очевидно, что для любого допустимого значения  выражение
выражение ![\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/ae843.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
А это и означает, что предел данной последовательности равен 0
4) 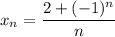

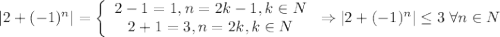
А значит, если взять ![N=\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/a4ca4.png) (**),
(**),  . И правда:
. И правда: ![\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|](/tpl/images/3820/0626/49458.png)
(**) Очевидно, что для любого допустимого значения  выражение
выражение ![\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/698f8.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
А это и означает, что предел данной последовательности равен 0
___________________________
2) a=1. Тогда 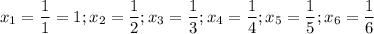
4)

___________________________
Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x. 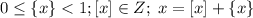

Сделаем замену:
пусть
Вернёмся к замене:
ответ: