1) После раскрытия скобок выражение принимает вид:
.
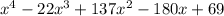Эта функция имеет 2 минимума:
1. (0,8; 1,8)
2. (10,2; -36).
2) Запишем пропорцию - a/b = c/d a = b + 6 c = d + 5
(b + 6) / b = (d + 5) / d Отсюда 6d = 5b d = 5b / 6
По условию a^2 + b^2 + c^2 + d^2 = 793
Подставив значения, получим - (b + 6)^2 + b^2 + (d + 5)^2 + d^2 = 793.
После раскрытия скобок - 2b^2 + 12b + 2d^2 + 10d + 61 = 793/
Заменив d = 5b / 6 и приведя к общему знаменателю, получим
72b^2 + 432b + 50b^2 + 300b = 26352 или 122b^2 + 732b - 26352 = 0
Корни этого уравнения равны -18 и 12. Отрицательное значение отбрасываем - b = 12.
а =12 + 6 = 18 - это первый член пропорции
натуральное число, тогда 
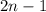будет натуральным и нечётным числом. Возведем данное число в квадрат: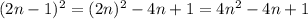
, 0 делиться на 8, следовательно условие выполняется.. Докажем что данное число делиться на 8 при 
:
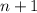делиться на 8. Следовательно, существует натуральный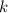 
так что: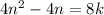
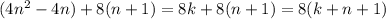следовательно, при 
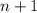данное число тоже делиться на 8. Ч.Т.Д.
1) Д = 49-4*4*(-7,5)=49+60=109
х1 =( 7-√109)/8
x2=(7+√109)/8
2) Д=100-4*25*1=100-100=0
х= -10/2*25=-10/50= -0,2
3)Д=9-4*3*4=9-48 - нет корней
4) Д = 1 -4*(-5)*1=1+20=21
х1=(-1-√21)/-10
x2=(-1+√21)/-10