ОДЗ вся числовая прямая
(x-3)(x+2)(x-7) =0
х-3=0, х= 3 или х+2=0, х=-2 или х-7=0, х=7
Отметим точки на прямой -2, 3, 7. знаки чередуются
(0; -2)и(3;7) отрицательная, (-2;3)и(7;0) положительная
![x^{4} -2x^{3} -x-2=0\\x^{3}(x-2)-x-2=0\\(x-2)(x^{3}-1)\\\\x-2=0\\x=2\\\\x^{3}-1=0\\x=\sqrt[3]{1}=1](/tpl/images/1657/7749/79f57.png)
Объяснение:
Линейное уравнение просто иксы в одну сторону, числа в другю.
Пример: x+3=0
Квадратное уравнение решается формулой (формула на картинке)
Общий вид: ax^2+bx+c=0
Кубическое уравнение решается формулой Кардано.
Общий вид: ax^3+bx^2+cx+d=0
А для уравнений выше кубической не существует общей формулы. Поэтому приходиться хитрить.
Сперва я вынес x^3 за скобку.

После таким же макаром вынес x-2 за скобку.
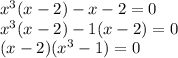
А уравнение такого вида называются распадающимися. Они решаются лекго. Уравнение примет значение ноль если один из множителей ноль.
Либо x-2 ноль, либо x^3-1=0.
А их просто решили.
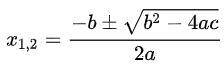
ОДЗ вся числовая прямая.
Приравняем функцию к 0 и составим уравнение (x-3)(x+2)(x-7) =0
Произведение равно 0, когда один из множителей равен 0, тогда:
х-3=0, х= 3
х+2=0, х=-2
х-7=0, х=7
Отметим точки на координатной прямой -2, 3, 7. Функция проходя через эти точки меняет знак.
ответ (00; -2)и(3;7) отрицательная, (-2;3)и(7;00) положительная