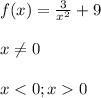
Тестовые интервалы | f(x) | f '(x) | Характер графика
---------------------------------------------------------------------------
x<0 + + возрастает
x=0 не определено вертикальная асимптота
x>0 + - убывает
cosα=-1/5, если α лежит в ІІІ четверти. - условие.
В задании нужно найти значение tg α , по определению тангенс угла - это отношение синуса этого угла к косинусу этого угла.
tg α = sin α/cosα
Таким образом, для нахождения тангенса α необходимо тнайти синус α , косинус α нам известен по условию.
Для нахождения синуса воспользуемся основным тригонометрическим тождеством:
sin ²α +cos²α =1 , отсюда выражаем sin ²α ⇒ sin ²α = 1-cos²α ,
sin ²α = 1-cos²α = 1- 1/25 = 24/25, sin α = - √24/5 = - 2√6/5.(ставим знак "-", поскольку sin α в ІІІ принимает отрицательные значения.)
tg α = sin α/cosα = - 2√6/5 : (-1/5) = 2√6.
разложим на множители знаменатель последней дроби
x^2-7x+12=0
D=49-48=1
x1=(7+1)/2=4
x2=(7-1)/2=3
следовательно x^2-7x+12=(х-4)(х-3)
приводим к общему знаменателю, решаем:
((x-4+x-3+x-2)-(x-3)(x-4)(x-2))/(x-2)(x-3)(x-4)<=0
расскроем скобки и приведем подобные в числителе:
3х-9-(х-3)(x^2-6x+8)=(x-3)(3-x^2+6x-8)=-(x-3)(x^2-6x+5)=-(x-3)(x-1)(х-5)
решаем неравенство
-(x-3)(x-1)(х-5)/(x-2)(x-3)(x-4)<=0
(x-3)(x-1)(х-5)/(x-2)(x-3)(x-4)>=0
изображая на числовой прямой эти корни, получаем
(-бесконечности;1]+(2;3)+(3;4)+[5;+бескон)
+это объединение промежутков.
D(y)=R
т.е. все действительные числа