Пусть  - канонический базис в
- канонический базис в 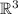 .
.
Тогда матрицу перехода 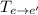 можно найти следующим образом:
можно найти следующим образом:
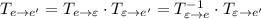
Если записать блочную матрицу 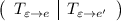 и привести путем элементарных преобразований к виду
и привести путем элементарных преобразований к виду  , то
, то 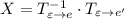
Матрицу 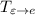 легко получить: достаточно записать в столбцы координаты векторов базиса
легко получить: достаточно записать в столбцы координаты векторов базиса  . Аналогично с матрицей
. Аналогично с матрицей 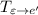 .
.
В итоге необходимо получить вид  следующей матрицы:
следующей матрицы:
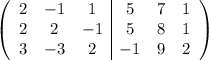
Вычтем первую строку из второй и третьей:
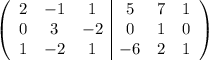
Вычтем из первой строки 2 третьих и поменяем их местами:
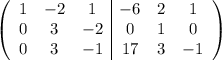
Вычтем из третьей строки вторую:
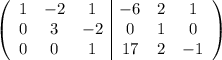
Прибавим ко второй строке 2 третьих и вычтем из первой третью:

Делим вторую строку на 3:
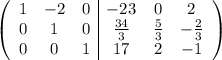
Прибавляем в первой строке 2 вторых:
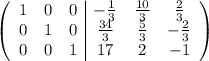
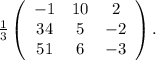
1. Известно, что 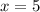 ,
, 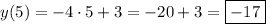
2. Известно, что 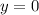 , тогда
, тогда 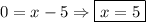
3. Обе точки имеют координаты 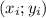 , причем при подставлении этих координат в уравнение функции, мы получаем верное равенство.
, причем при подставлении этих координат в уравнение функции, мы получаем верное равенство.
Смотрим на точку А: 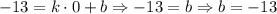
Отлично, уравнение известно теперь в таком виде: 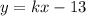 , в него подставим вторую точку и найдем
, в него подставим вторую точку и найдем 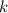 .
.
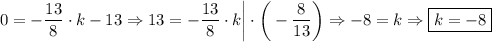
4. Решаем аналогично. Точка А: 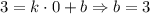
Уравнение уже в виде: 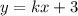
Точка B: 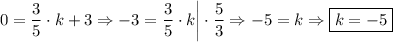
5. Условие симметрии относительно прямой 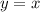 такое, что у функции
такое, что у функции 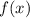 меняются местами область определения и область значений, то есть подставляя
меняются местами область определения и область значений, то есть подставляя 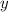 вместо
вместо  мы получаем по итогу
мы получаем по итогу  . При взаимно однозначном соответствии области определения и области значений (как в случае прямых) все вообще просто и работает везде.
. При взаимно однозначном соответствии области определения и области значений (как в случае прямых) все вообще просто и работает везде.
Что нужно сделать: есть 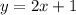 , делаем
, делаем
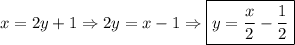
6=-5x+6
-5x=0
x=0
8=-5x+6
-5x=2
x=-0.4
100=-5x+6
-5x=94
x=-18.8