27.
Объяснение:
Пусть х - цифра из разряда десятков неизвестного двузначного числа,
у - цифра из разряда единиц этого числа,
тогда неизвестное двузначное число можно записать в виде:
(10х + у).
Утроенная сумма цифр этого числа будет иметь вид: (3(х + у)). =>
3(х + у) = 10х + у
Если поменять местами цифры искомого двузначного числа, то получим число: (10у + х). =>
10у + х - 45 = 10х + у.
Решим систему уравнений:
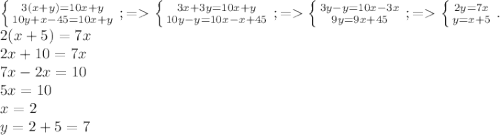
27 - искомое двузначное натуральное число.
Проверка:
3(2 + 7) = 27
3 * 9 = 27
27 = 27
72 - 27 = 45
2x-9>0⇒x>4,5
x∈(4,5;∞)
log(4)[(x²-9)/(2x-9)]=2
(x²-9)/(2x-9)=16
x²-9=16(2x-9)
x²-9-32x+144=0
x²-32x+135=0
D=1024-540=484
x1=(32-22)/2=5
x2=(32+22)/2=27