Алгебра: Или подскажите как это решать? : ) cos-(ctg²a+1)·sin²a

Или подскажите как это решать? : ) cos-(ctg²a+1)·sin²a

👇

Увидеть ответ

Ответ:

7Селестина

30.03.2020

Раскрой скобки и сведи все к одной переменной

4,7(4 оценок)

Открыть все ответы

Ответ:

Апслтел

30.03.2020

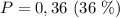
$P=0,36 $ $(36$ $\%)$

Объяснение:

Решим задачу через геометрическое определение вероятности.

Обозначим за х и у время прихода пассажиров:

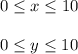
$0\leq x\leq 10\\\\0\leq y\leq 10$

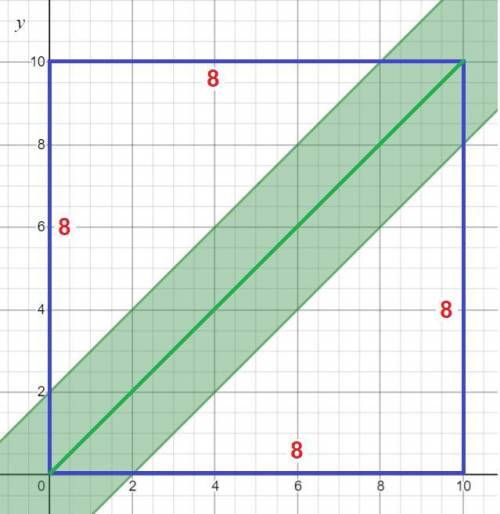
В прямоугольной системе координат этому условию удовлетворяют точки, лежащие внутри квадрата. Пассажиры встретятся, если между моментами их прихода пройдет не более 2 минут, то есть:

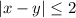
$|x-y| \leq 2$

Что равносильно следующей системе:

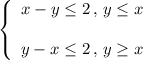
$\left\{\begin{array}{ccc}x-y\leq 2\, ,\,y\leq x\\\\y-x\leq2\, ,\,y\geq x \end{array}\right$

На графике такая область выглядит следующим образом (см. рисунок).

Тогда вероятность встречи равна отношению площади закрашенной области к площади всего квадрата.

Площадь закрашенной области равна разности площади квадрата и двух прямоугольных треугольников с катетами 10-2=8 .

Тогда:

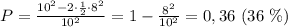
$P=\frac{10^2-2\cdot\frac{1}{2}\cdot8^2 }{10^2} =1-\frac{8^2}{10^2}=0,36 $ $(36$ $\%)$

До авіакаси у випадковий час у межах 10 хв звернулось 2 пасажири. Обслуговування одного пасажира три

4,7(12 оценок)

Ответ:

valya2612

30.03.2020

Особый вид средних величин - структурные средние - применяется для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен.
В качестве структурных средних чаще всего используют показатели моды - наиболее часто повторяющегося значения признака - и медианы - величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. В итоге у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой - не меньше его.
Если изучаемый признак имеет дискретные значения, то особых сложностей при расчете моды и медианы не бывает. Если же данные о значениях признака Х представлены в виде упорядоченных интервалов его изменения (интервальных рядов), расчет моды и медианы несколько усложняется.
Поскольку медианное значение делит всю совокупность на две равные по численности части, оно оказывается в каком-то из интервалов признака X. С интерполяции в этом медианном интервале находят значение медианы:
,
где XMe - нижняя граница медианного интервала;
hMe - его величина;
am/2- половина от общего числа наблюдений или половина объема того показателя, который используется в качестве взвешивающего в формулах расчета средней величины (в абсолютном или относительном выражении);
SMe-1 - сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала;
mMe - число наблюдений или объем взвешивающего признака в медианном интервале (также в абсолютном либо относительном выражении).
При расчете модального значения признака по данным интервального ряда надо обращать внимание на то, чтобы интервалы были одинаковыми, поскольку от этого зависит показатель повторяемости значений признака X. Для интервального ряда с равными интервалами величина моды определяется как

где ХMo - нижнее значение модального интервала;
mMo - число наблюдений или объем взвешивающего признака в модальном интервале (в абсолютном либо относительном выражении);
mMo-1 - то же для интервала, предшествующего модальному;
mMo+1 - то же для интервала, следующего за модальным;
h - величина интервала изменения признака в группах.2.Понятие об ошибке выборки Методы расчета ошибки выборки.
Под выборочным наблюдением понимается несплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергаются единицы изучаемой совокупности, отобранные случайным Выборочное наблюдение ставит перед собой задачу – по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов проведения статистического наблюдения и научно организованной работы по отбору единиц.
После проведения отбора для определения возможных границ генеральных характеристик рассчитываются средняя и предельная ошибки выборки.
Простая случайная выборка (собственно-случайная) есть отбор единиц из генеральной совокупности путем случайного отбора, но при условии вероятности выбора любой единицы из генеральной совокупности. Отбор проводится методом жеребьевки или по таблице случайных чисел.Типическая (стратифицированная) выборка предполагает разделение неоднородной генеральной совокупности на типологические или районированные группы по какому-либо существенному признаку, после чего из каждой группы производится случайный отбор единиц.

4,8(46 оценок)

Это интересно:

Компьютеры-и-электроника

17.08.2022

Как сделать сайт в Word: подробное руководство...

Здоровье

18.07.2020

Как нормализовать нерегулярный менструальный цикл: практические советы...

Кулинария-и-гостеприимство

10.04.2021

Пять советов, как приготовить вкусный холодный чай...

Образование-и-коммуникации