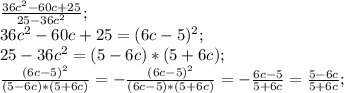
Числитель - сворачивается в квадрат разности, знаменатель - это разность квадратов.
Сворачивая по формуле квадрата разности числитель, и наоборот расписывая по разности квадратов знаменатель получаем вышесказаное выражение, далее, выносим минус за скобки, и в одной из скобок знаменателя меняем знак на противоположный, тем самым имеем право сократить с числителем. Далее, минус вносим в дробь, меняя знаки в числителе. Выходим на ответ.
Либо есть более короткий вариант решения, но тут нужна внимательность:
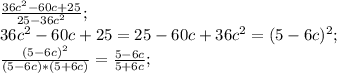
Т.к. это квадрат разности (В числителе) имеем право поменять местами 36c^2 и 25, сохраняя знаки. Свернется в тот-же самый квадрат разности, но нет заморочек с минусом.
Условия задачи приводят к системе двух уравнений с двумя неизвестными.
{a+b=12;
{ab=32.
Решаем подстановки.
{b=12-a;
{a(12-a)=32.
a²-12a+32=0
D=(-12)²-4·32=144-128=16=4²
a₁=(12-4)/2=4 или а₂=(12+4)/2=8
b₁=12-a₁=12-4=8 b₂=12-a₂=12-8=4
О т в е т. 4 и 8.