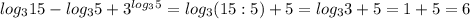
1. Б
Объяснение: Для умножения многочлена на многочлен существует очень легкое правило. Чтобы умножить два многочлена между собой, надо каждый член первого многочлена умножить на каждый член второго многочлена. После это полученные произведения сложить и привести подобные.
2. А
Объяснение: У вырази a*b е два множники, ''a''*b називається першим множником, а*''b'' називається другим множником.
3. В
Объяснение: Спрощуючи даний вираз, згрупуємо окремо числові та буквені множники.
4. Г
5. Б
Объснение: Коэффицие́нт «совместно» + «производящий») — термин, обозначающий числовой множитель при буквенном выражении, множитель при той или иной степени неизвестного, или постоянный множитель при переменной величине.
6. А
Решение
1) < 1 = 110° ; < 1 = < 3 = 110° , как вертикальные углы
<1 + <2 = 180° , как смежные, < 2 = 180° – 110° = 70°
<2 = <4 = 70° , как вертикальные углы
<4 = < 6 = 70° как внутренние накрест лежажие углы при параллельных прямых a и b и секущей с
<3 = <5 = 110° как внутренние накрест лежажие углы при параллельных прямых a и b и секущей с
<5 = <8 = 110° , как вертикальные углы
<6 = <7 = 700 , как вертикальные углы.
2) Пусть <2 = x , тогда <1 = x + 40.
По свойству смежных углов получаем уравнение
x + x + 40 = 180
2x = 140
x = 70
< 2 = 70°
< 1 = 70° + 40° = 110°
3) Сумма внутренних односторонних углов равна 1800.
<3 + <6 = = 180°
<3 - <6 = 70°
2*(<3) = 180° + 70°
2*(<3) = 250°
<3 = 125°
<6 = 180° – 125° = 55°
<1 = < 3 = 125° , как вертикальные углы
<1 + <2 = 180° , как смежные,
< 2 = 180° – 125° = 55°
<2 = <4 = 55° , как вертикальные углы
<4 = < 6 = 55° как внутренние накрест лежажие углы при параллельных прямых a и b и секущей с
<3 = <5 = 125° как внутренние накрест лежажие углы при параллельных прямых a и b и секущей с
<5 = <8 = 125° , как вертикальные углы
<6 = <7 = 55° , как вертикальные углы.