75.
Объяснение:
Пусть х - цифра в разряде единиц,
тогда (х + 2) цифра в разряде десятков.
Искомое двузначное число равно:
(х + 2) * 10 + х = 10х + 20 + х = 11х + 20.
Сумма цифр искомого двузначного числа равна:
х + х + 2 = 2х + 2.
Получаем уравнение:
(11х + 20) * (2х + 2) = 900
22x² + 22x + 40x + 40 = 900
22x² + 62x + 40 - 900 = 0
22x² + 62x - 860 = 0 I : 2
11x² + 31x - 430 = 0
D = 31² - 4 * 11 * (- 430) = 961 + 18920 = 19881
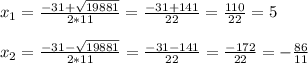
Второй корень не подходит, значит, цифра в разряде единиц равна 5.
Цифра в разряде десятков рана:
5 + 2 = 7.
Искомое двузначное число равно: 75.
Через точку M, принадлежащую биссектрисе угла с вершиной в точке О, провели прямую, перпендикулярную биссектрисе. Эта прямая пересекает стороны данного угла в точках A и B. Докажите, что AM=MB.
ОМ биссектриса ⇒ ∠АОМ = ∠ВОМ. Так как АВ ⊥ ОМ ⇒∠АМО = ∠ВМО = 90°
ОМ - сторона принадлежащая к обоим треугольникам. А значит:
ΔАОМ = ΔВОМ по свойству равенства треугольником (катет и прилежащий угол).
В равных треугольниках против равных углов лежат равные стороны ⇒ АМ = ВМ.