Пусть х км в час -скорость велосипЕдиста
y км в час - скорость мотоциклиста
встретились через 6 часов, значит велосипЕдист проехал 6х км,
мотоциклист проехал 6у км, а вместе они проехали 240 км
Первое уравнение:
6x+6y=240
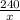 час потратил на весь путь велосипЕдист
час потратил на весь путь велосипЕдист
 час потратил на весь путь мотоциклист
час потратил на весь путь мотоциклист
велосипЕдист потратил на 5 часов больше чем мотоциклист
Второе уравнение
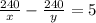
Решаем систему уравнений:
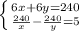



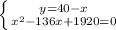

 138 не удовл смыслу задачи
138 не удовл смыслу задачи

О т в е т.
18 км в час -скорость велосипЕдиста
22 км в час - скорость мотоциклиста
х∈ (-11/3, -5/3)
Объяснение:
Решить двойное неравенство:
5 < -3x < 11
Двойное неравенство решается как система неравенств:
5 < -3x
-3x < 11
Первое неравенство:
5 < -3x
3х > -5
x < -5/3 (≈ -1,7)
x∈(-∞, -5/3), интервал решений первого неравенства.
Неравенство строгое, скобки круглые.
Второе неравенство:
-3x < 11
3х> -11
x > -11/3 (≈ -3,7)
x∈( -11/3, +∞), интервал решений второго неравенства.
Неравенство строгое, скобки круглые.
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем значения -11/3 (≈ -3,7), -5/3 (≈ -1,7).
Штриховка по первому неравенству от -5/3 влево до - бесконечности.
По второму неравенству штриховка от -11/3 вправо до + бесконечности.
Пересечение х∈ (-11/3, -5/3), это и есть решение системы неравенств.
a+5b=-20
a=-20-5b
b=(-20-a)/5