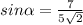следовательно 
Вариант 1
1. Представить в виде многочлена:
а) (b-5)(b-4)-3b(2b-3)
b²-4b-5b+20-6b+9b
-5b²+0+20
-5b²+20
б) 3x(x-2)-(x-3)²
3x²-6x-(x²-6x+9)
3x²-6x-x²+6x-9
2x²-9
в) 5(а+1)²-10а
5(а²+2а+1)-10а
5а²+10а+5-10а
5а²+5
2. Разложить на множители:
а) 3c³-75c
3c(c²-25)
3c(c-5)(c+5)
б) 3x²+6xy+3y²
3(x²+2xy+y²)
3(x+y)²
в) x³+8
x³+2³
(x+2)(x²-x*2+2²)
(x+2)(x²-2x+4)
3. Упростить выражение:
(y²+6y)²-y²(6+5y)(6-5y)-y²(12y-y²)
y⁴+12y³+36y²-y²(36-25y²)-12y³+y⁴
y⁴+12y³+36y²-36y²+25y⁴-12y³+y⁴
27y⁴
4. Разложить на множители:
а) (a-b)²-a²
(a-b-a)(a-b+a)
-b(a-b+a)
-b(2a-b)
б) x³+y³+2xy(x+y)
x³+y³+2xyx+2xy*y
x³+y³+2x²y+2xy²
5. Доказать, что если из квадрата нечетного числа вычесть 1, то результат будет делиться на 8:
Рассмотрим нечетное число как (2x - 1). Доказательство:
(2х - 1)² - 1 = 4х² - 4х + 1 - 1 = 4х² - 4х = 4*х*(х - 1) => данное выражение делится на 4, но т.к в 'х*(х-1)' одно число четное, значит данное выражение делится и на 2 => все это выражение делится на 8.
6. При любом натуральном n найдите остаток от деления выражения (n+1)(n+5)-(n-2)(n+2) на 6:
(n+1)*(n+5)-(n-2)*(n+2)=n²+6n+5-n²+4=6n+9.
(6n+9)/6=n+9/6=n+1,5, откуда ответ: 1,5
7. Решите уравнение:
(2x-1)(4x²+2x+1)-8x(x²+1)=3x+4
8x³-1-8x³-8x=3x+4
-1-8x=3x+4
-8x-3x=4+1
-11x=5
x= -5/11.
Надеюсь на лучший ответ, всего доброго!
а)Нам требуется составить сначала по-отдельности каждое уравнение, а затем каким-то образом скомбинировать их. Проще всего составить уравнение окружности. Его общий вид:
(x - x₀)² + (y - y₀)² = R², где (x₀;y₀) - координаты центра, R - радиус окружности. Теперь подставим всё в данное уравнение:
(x + 1)² + (y - 1)² = 144
Предлагаю перенести всё влево(хачем, будет ясно позднее):
(x + 1)² + (y - 1)² - 144 = 0
По условию, две прямые у нас касаются данной окружности и перпендикулярны оси y. Из последнего вытекает, что общее уравнение каждой прямой будет:
y = b. Осталось найти b.
Поскольку каждая прямая касается окружности, то она проходит непосредственно через конец радиуса. Нетрудно определить координаты этого конца. Это (-1;12+1), то есть (-1;13), а также (-1;11). Теперь можем составить уравнения каждой прямой:
y = 13, y - 13 = 0
y = 11, y - 11 = 0
Теперь скомбинируем ихю Для чего я перенёс всё влево в каждом уравнении? П(отому что мы получим произведениеЮ которое равно 0, значит оно задаёт комбинацию некоторых прямых. Итак, искомое уравнение:
((x + 1)² + (y - 1)² - 144)(y-13)(y-11) = 0