525 см в квадрате
Объяснение:
Обозначим длину разреза буквой x.Поскольку Ваня разрезал лист ватмана на два прямоугольника , то стороны этих прямоугольников , противоположные линии разреза, тоже равны x. Теперь сложим периметры двух этих частей . Мы получим периметр целого листа ватмана плюс удвоенную длину разреза, то есть 80 + 90 = 100 + 2x. Откуда x = 35 см. Посмотрим на первый прямоугольник. Его периметр 80 см, а сумма двух противоположных сторон равна 2 * 35 = 70 см.Значит,две другие его стороны в сумме дают 80 - 70 = 10 см.То есть каждая из них равна 10 : 2 = 5 см. Площадь этого прямоугольника равна 35 * 5 = 175 см в квадрате.
Точно так же найдем другие стороны второго прямоугольника. Получится (90 - 70) : 2 = 10 см. Значит, его площадь равна 35 * 10 = 350 см в квадрате.
Чтобы найти площадь целого листа ватмана, нужно просто сложить площади двух его частей. То есть площадь целого листа равна 175 + 350 = 525 см в квадрате.
Объяснение:
1.
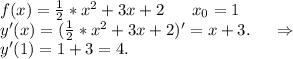
ответ: y'(1)=4.
2.

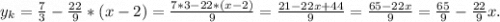
3.
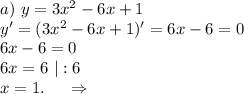
В окрестности точки x = 1 производная функции меняет знак с (-) на (+). Следовательно, точка x = 1 - точка минимума.
При х∈(-∞;1) функция убывает.
При х∈(1;+∞) фунуция возрастает .
![b)\ y=x^9-9x\\y'=(x^9-9x)'=9x^8-9=9*(x^8-1)=0\\9*(x^8-1)=0\ |:9\\x^8-1=0\\x^8=1\\x=\sqrt[8]{1}\\x_1=-1\ \ \ \ x_2=1](/tpl/images/1848/3010/401ca.png)
В окрестности точки x = -1 производная функции меняет знак с (+) на (-). Следовательно, точка x = -1 - точка максимума.
При х∈(-∞;-1) фунуция возрастает .
В окрестности точки x = 1 производная функции меняет знак с (-) на (+). Следовательно, точка x = 1 - точка минимума.
При х∈(1;+∞) функция возрастает. ⇒
При х∈(-1;1) функция убывает.