x^2+8x+16=0
Находим дискриминант D=64-4*16=0
D=0, значит ур-е имеет одно решение
x=-8/2=-4
Відповідь:
Пояснення:
1.
а) ні
б) так
в) ні
г) так
=========================
2.
а) y = -3x + 2 при x = 5, y - ?
y = -3 * 5 + 2 = -15 + 2 = -13
б) y = -3x + 2 при y = 8, x - ?
8 = -3x + 2
3x = 2 - 8 = -6
x = -6/3 = -2
=========================
3. на фото нижче
=========================
4. y = -0,2x + 1,8
а) нулі функції - ?
0 = -0,2x + 1,8
0,2x = 1,8
x = 1,8/0,2 = 9
б) N(-6; -3), де x = -6, y = -3
-3 = -0,2*-6 + 1,8 = 1,2 + 1,8 = 3 - неправда, а це означає що графік не проходить через точку N.
=========================
5.
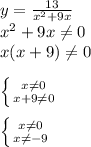 Відповідь: х∈(-∞;-9)∪(-9;0)∪(0;+∞)
Відповідь: х∈(-∞;-9)∪(-9;0)∪(0;+∞)
=========================
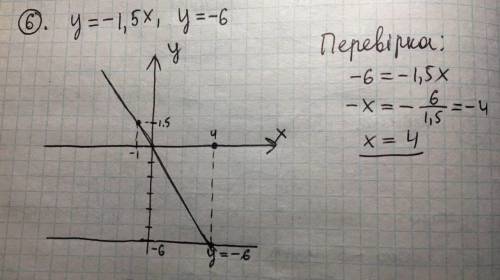
6. на фото нижче
=========================
7. на фото нижче
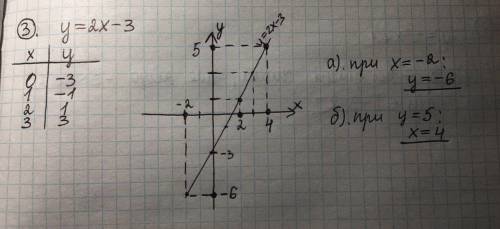
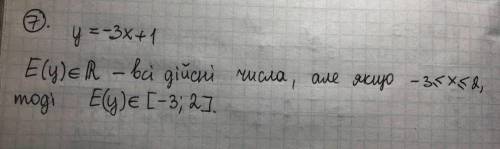
1
Объяснение:
Угол наклона прямой в координатной плоскости изменяется в промежутке [0; π) за исключением π/2, то есть по значению тангенса можно однозначно определить угол. Вспомним, что прямые параллельны, если соответственные углы равны. Если принять за секущую ось Ox, то можно сравнить углы наклона. А для этого уже достаточно сравнить их тангенсы!
Тангенс угла наклона касательной можно найти с производной — это значение производной в данной точке. Тангенс угла наклона прямой — это коэффициент перед x. Тогда:
 — если подставить вместо x какое-то значение, получим тангенс угла наклона касательной. Тангенс угла наклона прямой — это 1 (y = 1*x + 8). Поэтому, чтобы прямые были параллельны, нужно приравнять производную и тангенс угла наклона прямой:
— если подставить вместо x какое-то значение, получим тангенс угла наклона касательной. Тангенс угла наклона прямой — это 1 (y = 1*x + 8). Поэтому, чтобы прямые были параллельны, нужно приравнять производную и тангенс угла наклона прямой:
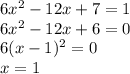
дискриминант=64-64=0
-8/2=-4
х=-4