1. нет; 2. 1) общего вида 2) общего вида 3) общего вида 3. 1) -1; 3 2) 1; -3 4) -1
Объяснение:
1. Если функция нечетная то произведение f(3)f(-3) не будет положительным.
2.
1)
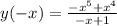
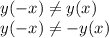
Это функция общего вида
2)
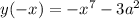
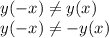
Это функция общего вида
3)
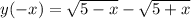
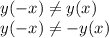
Это функция общего вида
3.
1)
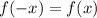
Значит
![min_{[2;4]}f(x)=min_{[-4;-2]}f(x)=-1\\max_{[2;4]}f(x)=max_{[-4;-2]}f(x)=3](/tpl/images/3904/3705/69e2d.png)
2)
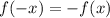
Значит
![min_{[2;4]}f(x)=-min_{[-4;-2]}f(x)=1\\max_{[2;4]}f(x)=-max_{[-4;-2]}f(x)=-3](/tpl/images/3904/3705/5cc0f.png)
4.
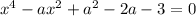
Это биквадратное уравнение. Делаем подстановку
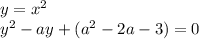
Уравнение будет иметь один корень, когда дискриминант равен 0
Но, поскольку х=±√у, то при любом положительном у мы получим два различных значения х. Одно значение х мы получим лишь в случае у=0. Тогда х=√0=0. Следовательно
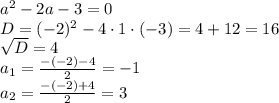
Делаем проверку:
1) а=-1
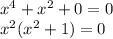
Имеется одно решение (т.к выражение в скобках никогда не будет равно 0)
2) а=3
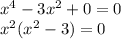
Здесь появляется второй корень. Значит, это значение не подходит.
Окончательно получаем решение: а=-1
5x^2+3x-2 / 10x^2+x-2
Решим каждое выражение по формуле дискриминанта:
5x^2+3x-2=0
D= 9+40=49
корень из D=7
x1= -3-7/10= -1
x2= -3+7/10= 0,4
Используя это, выражение можно представить так: (впереди всегда ставится первый коэфицент, в данном случае 5, а остальное раскладываем на скобки ... затем пять умножаем на вторую скобку, чтобы избавиться от дроби 0,4)
5x^2+3x-2= 5(x+1)(x-0,4)= (x+1)(5x-2)
Тоже самое делаем со вторым выражением:
10x^2+x-2=0
D=1+80=81
корень из D=9
x1= -1-9/20= -0,5
x2= -1+9/20= 0,4
Тут все так же. Впереди 10, но мы раскладываем десятку на 2 и 5, и умножаем на "удобные" скобки, чтобы избавиться от дробей.
10x^2+x-2= 10(x+0,5)(х-0,4)= (2х+1)(5х-2)
Заменяем данные выражения - получившимися:
(х+1)(5х-2) / (2х+1)(5х-2)= х+1 / 2х+1
При делении скобка (5х-2) сократится.
Окончательный ответ дробь х+1 / 2х+1
Это все :) Объяснила, как смогла, удачи))
Если что, во вложениях формулы для решения дискриминанта!

41/20*200/1=сокращаем и получается 410