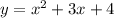
Найдем уравнение касательной, проходящей через точку с абсциссой 
Для этого найдем производную данной функции:

Найдем значение функции в точке с абсциссой  :
:

Найдем значение производной данной функции в точке с абсциссой  :
:
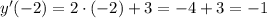
Уравнение касательной имеет вид:
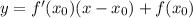
Подставим значение 

Итак, уравнение касательной заданной функции: 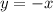
Воспользуемся геометрическим смыслом касательной: коэффициент наклона  касательной
касательной 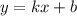 численно равен тангенсу угла наклона
численно равен тангенсу угла наклона 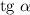 с положительным направлением оси
с положительным направлением оси 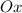
В найденной касательной коэффициент 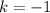 , следовательно,
, следовательно, 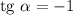 при
при  или
или 
ответ:  или
или 
По определению логарифма 1-2Х<2 в нулевой степени
-2Х<1
X>-1/2
Сравнивая с ОДЗ, получим -1/2<X<1/2