№6
3х – 5 (2х + 1) = 3 ( 3 – 2х)
3х–10х–5=9–6х
3х–10х+6х=9+5
–х=14
х=–14
ответ: –14
№5
х²–3х–3у–у²= –3(х+у)+х²–у²= –3(х+у)+(х+у)(х–у)= (х+у)(–3+х–у)
№1
(а +6)²–2а(3 – 2а)=а²+12а+36–6а+4а²= 5а²+6а+36
№2
Система:
5х – 2у = 11
4х – у = 4 |*(–2)
Система:
5х – 2у = 11 (Ур 1)
–8х+2у=–8 (Ур 2)
Сложим уравнения 1 и 2, получим:
–3х=3
х=–1
Подставим значение х у уравнение 1, получим:
5*(–1)–2у=11
–5–2у=11
–2у=16
у=–8
ответ: х=–1; у=–8
№4
Пусть х км– путь в третий день, тогда во второй х+5, а в первый (х+5)+10
Составим уравнение:
х+(х+5)+(х+5+10)=50
х+х+5+х+5+10=50
3х=50–10–5–5
3х=30
х=10
Тогда в третий день 10 км, во второй 10+5=15 км, в первый 10+5+10=25 км
ответ: Первый день 25 км; второй день 15 км; третий день 10 км.
№3
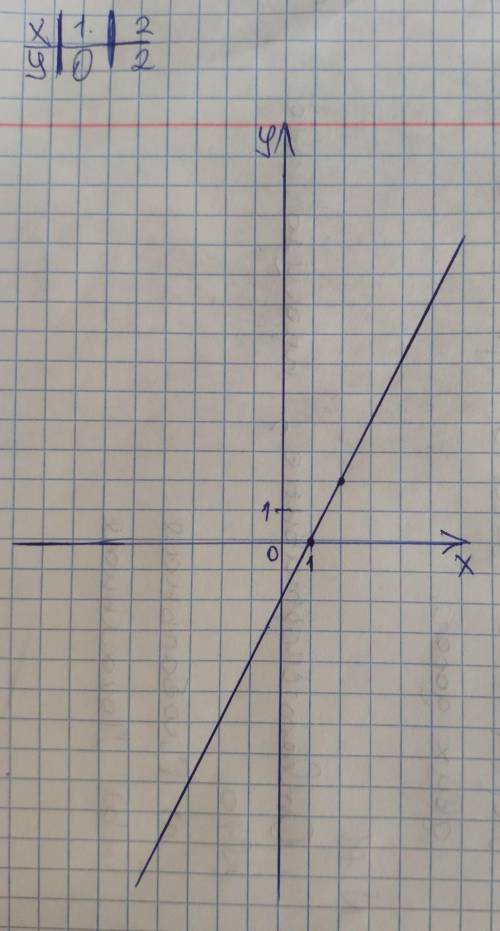
Кординаты точки А х=–10; у=–20.
Подставим значения в функцию у = 2х – 2, получим:
–20=2*(–10)–2
–20=–20–2
–20≠–22
Следовательно график НЕ проходит через точку А.
График во вложении
ответ:Линейной функцией называется функция вида y = k * x + b, где x – независимая переменная, k и b – любые числа.
а) Рассмотрим функцию у = (4 * х – 7) : 2. Перепишем формулу данной функции в виде у = (4 * х) : 2 – 7 : 2 = 2 * х – 3,5. Ясно, что если принять k = 2 и b = –3,5, то получаем вид линейной функции из п. 1. Следовательно, данная функция является линейной функцией.
б) Рассмотрим функцию у = 3 * (х + 8). Перепишем формулу данной функции в виде у = 3 * х + 3 * 8 = 3 * х + 24. Ясно, что если принять k = 3 и b = 24, то получаем вид линейной функции из п. 1. Следовательно, данная функция является линейной функцией.
в) Рассмотрим функцию у = х * (6 – х). Перепишем формулу данной функции в виде у = х * 6 – х * х = 6 * х – х². Данная функция не является линейной функцией, так как в её составе наряду с линейным выражением (6 * х) имеется и нелинейное выражение (–х²).
г) Рассмотрим функцию у = х * (9 – х) + х². Перепишем формулу данной функции в виде у = х * 9 – х * х + х² = 9 * х. Ясно, что если принять k = 9 и b = 0, то получаем вид линейной функции из п. 1. Следовательно, данная функция является линейной функцией.
Объяснение:
sqr-квадратный корень