Объяснение:
Надо найти сколькими из 4-х человек можно отобрать 2, то есть найти число сочетаний из 4 по 2 - это будет . Решение на картинке.
Если объяснять словами то есть 4 человека 1,2,3,4. В первый отряд мы можем взять (1 и 2), (1 и 3), (1 и 4), (2 и 3), (2 и 4), и (3 и 4) - это и будет .
Теперь найдем сколькими можно сочетать оставшиеся 12 человек по 6, то есть сколькими можно их разделить на 2 равных отряда. Это . Решение на второй картинке.
И, что бы окончательно решить, сколькими можно распределить 12 человек не знающих местность и 4 человек знающих местность нужно перемножить полученные результаты:
6*66 = 396 - это и будет общее количество , которыми можно разделить 16 человек на 2 отряда по 8 человек, что бы в каждом отряде было 2 человека знающих местность и 6 человек не знающих местность.

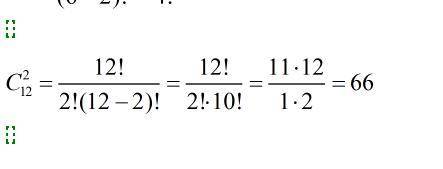
1) Так как существует точка (1;1), то а+b+с=1. Так как при X=2, будет то же значение, то 4a+2b+c=1. Теперь получаем два уравнения. Если из второго вычесть первое, то получим 3a+b=0. b=-3a. Подставив в первое уравнение, получаем, что a-3a+c=1. с=1+2a. Так как в точке x=(-b)/(2a) - вершина параболы, то x=-(-3*a)/(2a). x=3a/(2a). x=1,5. Это парабола, у которой ветви направлены вниз, так как существует наибольшее значение. Это значение достигается на вершине параболы при x=1,5 и y=3. Подставив эти значения в квадратное уравнение, получаем 3=2,25a+1,5b+c. Заменим b и c через a. 3=2,25a+1,5*(-3a)+1+2a. Упрощаем и находим a. 3=2,25a-4,5a+1+2a. 2=2,25a-4,5a+2a. 2=-0,25a. a=-8. Это значение должно быть отрицательным, так как ветви параболы напрвлены вниз. b=-3*a. b=-3*(-8). b=24. c=1+2*(-8). c=-15.
2) Двузначное число можно представить в виде 10*a+b, где a и b будут однозначными цифрами в позиционной системе счисления. Так происходит деление на сумму этих чисел, то это выражается в виде (10*a+b)=7*(a+b)+6. Деление на произведение (10*a+b)=3*(a*b)+11. Из первого уравнения получаем 10*a+b=7*a+7*b+6. 3*a-6*b=6. Сокращаем обе части на 3. Получаем a-2*b=2, a=2+2b. Упростим тепрь второе уравнение 10a+b=3ab+11. Подставим значение а из полученного во второе уравнение. 10(2+2b)+b=3(2+2b)b+11. 20+21b=6b+6b^2+11. Придется решать квадратное уравнение. 6b^2-15b-9=0. D=15^2-4*6*(-9). D=225+216. D=441. D=21^2. b=(15+21)/2/6. Здесь вариант с минусом убирается так как b - только положительное число. b=36/2/6. b=3. Значит a= 2+2b. a=2+6. a=8. Исходное число будет равно 83.