силий Тёркин»? Назовите подзаголовок поэмы. 3. Почему поэт пишет, что «на войне сюжета нету» и что книга «без начала и конца»? 4. Во для анализа главы «Переправа»: а) На какие части разделяют главу слова «Переправа, переправа...»? Каким настроением проникнута каждая часть главы? С какой интонацией следует читать эти строки? б) Что является «лейтмотивом» данной главы? Почему? в) Каким в этой главе предстаёт перед читателем Василий Тёркин? 5. Во для анализа главы «О награде»: а) Как построена эта глава? Дайте характеристику частей этой главы? б) Как проявляется здесь стилевое многообразие поэмы? в) Что нового об образе Тёркина мы узнаём в этой главе? г) Можем ли сказать, что автор сроднился с Тёркиным? В чём это проявляется? Что значит слово «родина» для каждого из них? е) Выделите в главе строки, которые являются рефреном произведения. Как вы думаете, почему именно такой рефрен включён Твардо
Объяснение:
По определению, 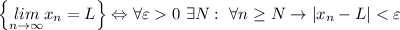
Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение 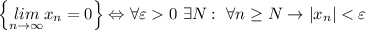
2) 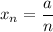
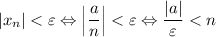
А значит, если взять ![N=\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/0d89e.png) (*),
(*),  . И правда:
. И правда: 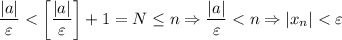
(*) Очевидно, что для любого допустимого значения  выражение
выражение ![\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/ae843.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
А это и означает, что предел данной последовательности равен 0
4) 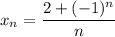

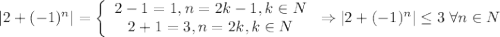
А значит, если взять ![N=\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/a4ca4.png) (**),
(**),  . И правда:
. И правда: ![\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|](/tpl/images/3820/0626/49458.png)
(**) Очевидно, что для любого допустимого значения  выражение
выражение ![\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/698f8.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
А это и означает, что предел данной последовательности равен 0
___________________________
2) a=1. Тогда 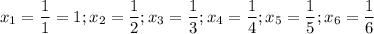
4)

___________________________
Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x. 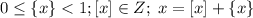

a) cosx-sinx f'(0)=1
в) 2x(x^3+x)+(x^2-1)(3x^2+1)=2x^4+2x^2+3x^4-1-2x^2=5x^4-1
5*(-1)^4-1=5-1=4
г)7/(2sqrt(7x-3))
7/(2sqrt(7-3))=7/4