




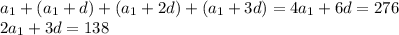
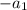 при делении на 3, значит разность
при делении на 3, значит разность  дает остаток
дает остаток 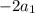 при делении на 3, но их разность кратна 3. Поэтому первое число кратно 3.
при делении на 3, но их разность кратна 3. Поэтому первое число кратно 3.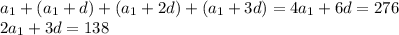
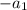 при делении на 3, значит разность
при делении на 3, значит разность  дает остаток
дает остаток 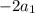 при делении на 3, но их разность кратна 3. Поэтому первое число кратно 3.
при делении на 3, но их разность кратна 3. Поэтому первое число кратно 3.
Проверим, делится ли левая часть на ( х +7)( +-7 - делители числа 21)
Делить будем "углом":
х³ +9х² + 11х -21 |(x +7)
x³ +7x² x² + 2x - 3
2x² + 11x
2x² + 14 x
-3x -21
-3x -21
х³ +9х² + 11х -21 = (x² +2x -3)(x +7) = (x + 3)(x - 1)(x + 7)
наше уравнение : (x + 3)(x - 1)(x + 7)=0⇒
⇒ х + 3 = 0 ⇒ х = -3; 1; -7
х - 1 = 0
х + 7 = 0
б) (с - 3)(4с² -20 с +25) = 0
(с - 3)((2с -5)² = 0
с - 3 =0 ⇒ с = 3
2с - 5 = 0 ⇒ с = 2,5
2) x^4 -10x^3 +35x^2 -50x +24=0
(x -4)(x^3 -6x^2 +11x -6) = 0
(x -4)(x -3)(x -2)(x -1) = 0
как это получилось? я многочлен разделил "углом" на (х -4)
получил в ответе х³ - 6х² +11х - 6. теперь этот результат надо разложить на множители:
(х³ - 6х² +11х) - 6 = х( х² -6х + 9 - 9 +11) -6=
=х((х-3)² +2) - 6= х(х-3)² + 2х -6=х(х-3)² + 2(х-3)=
=(х-3) ( х(х-3) +2) = (х-3)(х² -3х +2) = (х-3) (х-1)(х-2)
Теперь можно решать:
(x -4)(x -3)(x -2)(x -1) = 0
х = 4; 3; 2; 1
3) числитель = 6^6·2^3 - 3^6 = (2·3)^6·2^3 - 3^6=
= 2^6·3^6·2^3 - 3^6= 3^6(2^9 -1)= 3^6·(512 -1) = 3^6·511
знаменатель = 6^6 +6^3·3^3 + 3^6 =
=(2·3)^6 + (2·3)3·3^3 +3^6 = 2^6·3^6 + 2^3·3^3·3^3 + 3^6=
=2^6·3^6 +2^3·3^6 +3^6 = 3^6(2^6 +2^3 +1)= 3^6(64+8 +1) =
=3^6·73
ответ:7