Кусочно- заданная функция - это функция , которая на различных промежутках оси ОХ задаётся разными функциями. ( Как бы на разных "кусочках" оси ОХ задаются разные функции).
На промежутке (-∞ ; -2 ] функция представляет из себя гиперболу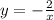 
. График гиперболы рисуем только на этом промежутке (сплошной линией), оставшаяся часть графика на промежутке (-2 ; +∞) стирается (либо рисуется пунктирной линией). Точка с абсциссой х= -2 , точка (-2,1) , принадлежит этому графику.
На промежутке (-2 ; 2] рисуем график у=|x|-1 . Это график функции у=|x|, который смещён на 1 единицу вниз по оси ОУ. Точка (-2,1) не принадлежит графику, а точка (2, 1) принадлежит графику.
На промежутке (2 ; + ∞) рисуем график функции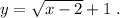 
Это график функции 
, смещённый вдоль оси ОХ на 2 единицы вправо и вдоль оси ОУ на 1 единицу вверх . Точка (2,1) не принадлежит графику функции.
График кусочно заданной функции нарисован сплошными линиями.
(3 1/3; 3)
Объяснение:
Система уравнений:
(6-x)²+(-3-y)²=4/9 ·97
(x-2)²+(y-6)²=97/9; 4(x-2)²+4(y-6)²=4·97/9
(6-x)²+(-3-y)²-4(x-2)²-4(y-6)²=4/9 ·97 -4·97/9
(6-x)²-(2x-4)²+(3+y)²-(2y-12)²=0
(6-x-2x+4)(6-x+2x-4)+(3+y-2y+12)(3+y+2y-12)=0
(10-3x)(2+x)+(15-y)(3y-9)=0
10-3x=0; 3x=10; x₁=10/3
2+x=0; x₂=-2
15-y=0; y₁=15
3y-9=0; 3y=9; y=9/3; y₂=3
Проверка:
при x₁=10/3 и y₁=15
(10/3 -2)²+(15-6)²=97/9
(10/3 -6/3)²+81=97/9
9·16/9+9·81=97 - равенство не выполняется, так как уже 9·81>97, следовательно, корень y₁ к данной системе вообще не подходит;
при x₁=10/3 и y₂=3
(10/3 -2)²+(3-6)²=97/9
9·16/9 +9·9=97
16+81=97- равенство выполняется;
при x₂=-2 и y₂=3
(-2-2)²+(3-6)²=97/9
9(16+9)=97
9·25≠97 - равенство не выполняется, так как 9·25>97.
Отсюда следует, что единственными корнями являются:
x₁=10/3=3 1/3 и y₂=3.
Основное условие того, чтобы функция была обратимой- она должна быть монотонная на всем промежутке. Для Этого нам дали условие что х>0
выражаем х:
-x^2=y-2
x^2=-y+2
x=корень из (-y+2)
переобозначим, вместо х напишем у, и наоборот, получаем:
y=корень из(-x+2) -это и есть обратная функция
Т.к. х положительный, то корень также будет со знаком +