2sinx-cos^2x*sinx=0
sinx(2-cos^2x)=0
1)sinx=0
x=πk, k∈Z
2)2-cos^2x=0
cos^2x=2
cosx=±√2
x=±arccos(±√2)+2πk, k∈Z
Объяснение:
Тоғызқұмалақ ойынындағы тактикалық әрекеттер
Тоғызқұмалақ ойынында қарымта жүріс жасаған ойыншыны қалай атайды?
Артқа
Тексеру
Тоғызқұмалақ ойынындағы тактикалық әрекеттер
Тоғызқұмалақ ойынындағы жалпы құмалақтар саны қанша болады?
176
144
182
162
168
Артқа
Тексеру
Тоғызқұмалақ ойынындағы тактикалық әрекеттер
Тоғызқұмалақ ойынындағы жалпы құмалақтар саны қанша болады?
176
144
182
162
168
Артқа
Тексеру
Тоғызқұмалақ ойынындағы тактикалық әрекеттер
Тоғызқұмалақ ойынындағы жалпы құмалақтар саны қанша болады?
176
144
182
162
168
Артқа
Тексеру
Тоғызқұмалақ ойынындағы тактикалық әрекеттер
Тоғызқұмалақ ойынындағы жалпы құмалақтар саны қанша болады?
176
144
182
162
168
Артқа
Тексеру
Тоғызқұмалақ ойынындағы тактикалық әрекеттер
Тоғызқұмалақ ойынындағы жалпы құмалақтар саны қанша болады?
176
144
182
162
168
Артқа
Тексеру
При любом а, b и с график функции y=x^3 + ax^2 + bx+c имеет центр симметрии
Объяснение:
Решение в приложении
У кубической параболы будет всего один центр симметрии. В точке с абсциссой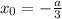 
ординатой 
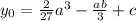. Эта точка совпадает с точкой перегиба.
Если посмотреть скриншоты, то только в случае 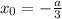выполняется условие центра симметрии.
Это можно было бы доказать с параллельного переноса, растяжения и сжатия, поворота кубической параболы y=x³. Любая другая парабола получается из исходной с этих преобразований.
Интересно еще вот что, в формуле Кардано для решения кубического уравнения первая подстановка именно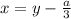 
.
I.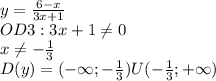
II. 2sinx-cos^2x*sinx=0
sinx(2-cos^2x)=0
1)sinx=0
x=pik . k=z
2)2-cos^2x=0
cos^2x=2
cosx=+-√2
x=+-arccos(+-√2)+2pik . k=z