Тут все очень просто, существуют такие уравнения, на одну формулу, где вводится переменная R=√(A^2+B^2).
Где:
Asina+Bcosa=Rsin(a+f);
А период получится разным, смотря во что сворачивать, если в синус, там никак не получится 2pik, а если по косинусу, то да. Смотри все на скриншоте.
Если что, меня найдешь по почте.
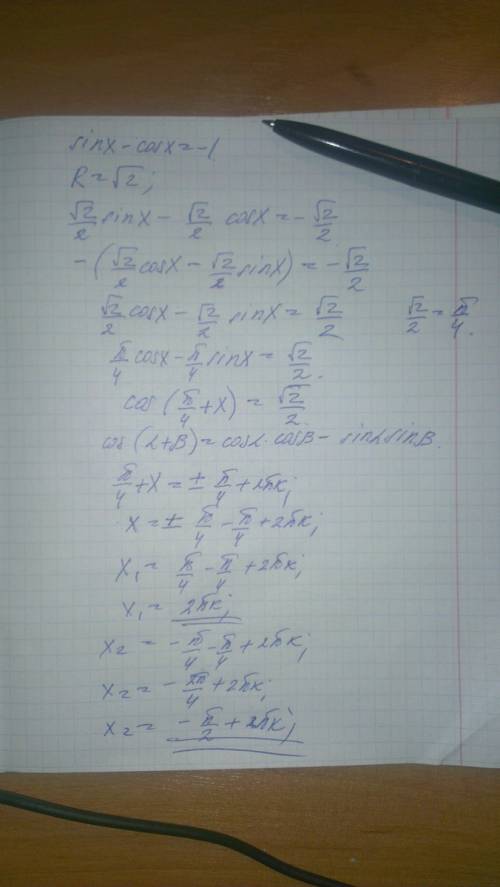
a=4
(2;1)
Объяснение:
Из условия известно, что первое уравнение этой системы обращается в верное равенство при x= 8 и y= −7; тогда, подставив эти значения переменных в первое уравнение, можно найти коэффициент a.
Получим:
ax+3y=11;8a+3⋅(−7)=11;8a=11−(−21);8a=32;a=4.
При таком значении коэффициента a данная система примет вид:
{4x+3y=115x+2y=12
Для решения этой системы уравнений графически построим в одной координатной плоскости графики каждого из уравнений.
Графиком уравнения 4x+3y=11 является прямая.
Найдём две пары значений переменных x и y, удовлетворяющих этому уравнению.
x −1 2
y 5 1
Построим на координатной плоскости xОy прямую m, проходящую через эти две точки.
Графиком уравнения 5x+2y=12 также является прямая.
Найдём две пары значений переменных x и y, удовлетворяющих этому уравнению.
x 0 2
y 6 1
Построим на координатной плоскости xОy прямую n, проходящую через эти две точки.
Получим:
Прямые m и n пересекаются в точке A, координаты которой являются решением системы, т. е. A(2;1)
Объяснение:
Вовсе не сложный пример. Опять же решай по дополнительному углу. Получается твой ответ( зря даёшь в дано ответ =Ъ)) Так не интересно