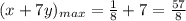(см. объяснение)
Объяснение:
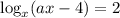
ОДЗ:
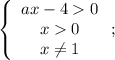
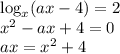
Заметим, что для любого корня уравнения вне зависимости от значения параметра  произведение
произведение 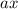 будет больше или равно 4.
будет больше или равно 4.
Причем 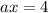 , если
, если 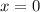 - корень уравнения. Но это невозможно, так как при
- корень уравнения. Но это невозможно, так как при 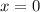 имеем
имеем 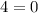 (неверно) при любом значении параметра.
(неверно) при любом значении параметра.
Тогда 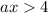 , то есть условие ОДЗ
, то есть условие ОДЗ  будет выполнятся всегда.
будет выполнятся всегда.
Исходное уравнение будет иметь ровно один корень, либо если 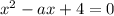 имеет один корень, удовлетворяющий ОДЗ, либо если это уравнение имеет два корня, только один из которых удовлетворяет ОДЗ.
имеет один корень, удовлетворяющий ОДЗ, либо если это уравнение имеет два корня, только один из которых удовлетворяет ОДЗ.
Рассмотрим первый случай. Он достижим, когда 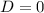 .
.
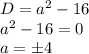
При 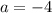 уравнение имеет корень
уравнение имеет корень  , поэтому такое значение параметра не подходит.
, поэтому такое значение параметра не подходит.
При 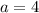 уравнение имеет корень
уравнение имеет корень 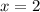 , поэтому такое значение параметра подходит.
, поэтому такое значение параметра подходит.
Рассмотрим второй случай. Он достижим, когда 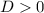 .
.
Здесь также важно, чтобы уравнение либо имело один корень  , а другой положительный, либо один корень неположительный, а другой положительный, не равный единице.
, а другой положительный, либо один корень неположительный, а другой положительный, не равный единице.
Обратимся к первой ситуации:
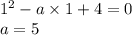
В этом случае уравнение имеет корни  или
или 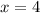 , первый из которых, отпадая, обеспечивает наличие единственного корня у исходного уравнения. Тогда такое значение параметра подходит.
, первый из которых, отпадая, обеспечивает наличие единственного корня у исходного уравнения. Тогда такое значение параметра подходит.
Для того чтобы вторая ситуация могла быть достижимой, необходимо, но не достаточно, чтобы выполнялось условие 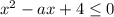 при
при 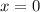 . Однако это невозможно, поэтому такой вариант рассматривать дальше не будем.
. Однако это невозможно, поэтому такой вариант рассматривать дальше не будем.
Итого при 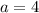 или
или  исходное уравнение имеет единственное решение.
исходное уравнение имеет единственное решение.
Задание выполнено!
ответ: 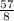
Объяснение:
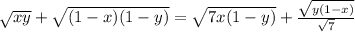
Поскольку:
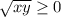
То 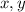 либо имеют одинаковые знаки, либо один из них равен
либо имеют одинаковые знаки, либо один из них равен  , но поскольку нас интересует наибольшее значение:
, но поскольку нас интересует наибольшее значение: 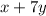 , то целесообразно рассматривать:
, то целесообразно рассматривать:
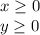
Откуда, с учетом ОДЗ имеем:
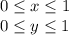
Поскольку левая и правая часть равенства положительны, то после возведения в квадрат получаем равносильное уравнение ( в данном случае все радикалы не могут быть одновременно равны  , также не трудно заметить, что удвоенные произведения в левой и правой части одинаковы и равны
, также не трудно заметить, что удвоенные произведения в левой и правой части одинаковы и равны 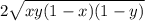 , поэтому они уничтожаться)
, поэтому они уничтожаться)
Откуда, получим:

Применим такой хитрый прием, вычтем из обеих частей равенства удвоенное произведение 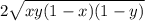 , но тогда слева и справа имеем квадрат разности:
, но тогда слева и справа имеем квадрат разности:
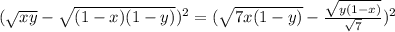
Оно равносильно совокупности двух уравнений:

То есть уравнение:
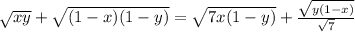
равносильно совокупности двух уравнений, что представлены выше.
То есть, у него с каждым из двух уравнений выше есть общие корни.
Причем, в сумме эти общие корни дают множество корней исходного уравнения.
Cложим исходное уравнение с первым:
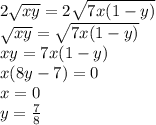
В полученном уравнении некоторые зависимости совпадают с зависимостями в исходном уравнении, причем хотя бы одна зависимость подойдет.
Сложим исходное уравнение со вторым:

То есть, если уравнение имеет корни, то их надо искать из множества:
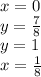
Все корни подходят по ОДЗ.
Подставим 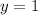 :
:
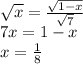
Пара подходит и рассматривать дальнейшие пары нет смысла, ибо
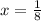 - наибольшее
- наибольшее  из возможных, а
из возможных, а 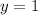 - наибольшее
- наибольшее 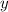 из возможных.
из возможных.
Таким образом, наибольшее значение: