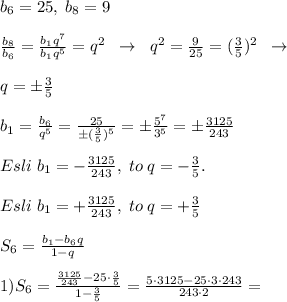
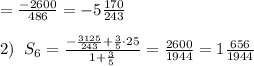
№412.
Пусть имеется х кг апельсинов. В пакет вмещается х/3 кг, в коробку - х/5 или х/3-2 кг. Составим и решим уравнение:
х/5=х/3-2 |*15
3x=5х-30
5х-3х=30
2х=30
х=30:2
х=15
ответ: имеется 15 килограммов апельсинов.
№413(б).
Пусть n - первое нечётное число, тогда два последующих нечётных числа - (n+2) и (n+4). Их сумма равна n+n+2+n+4 или 69. Составим и решим уравнение:
n+n+2+n+4=69
3n=69-6
3n=63
n=63:3
n=21
n+2=21+2=23
n+4=21+4=25
ответ: да, это числа 21, 23 и 25.
№414(б).
Пусть купили х линеек, тогда кистей купили (х+7), а карандашей - 4х. Всего купили х+х+7+4х или 43 предмета. Составим и решим уравнение:
х+х+7+4х=43
6х=43-7
6х=36
х=36:6
х=6
х+7=6+7=13
4х=4*6=24
ответ: купили 6 линеек, 13 кистей и 24 карандаша.
Чтобы найти наибольшее значение на отрезке, нужно найти экстремумы функции и сравнить их со значенями функции на концах отрезка. Подозрительные на экстремум точки - это точки, в которых производная функции равна нулю. Найдем производную и выясним, в каких точках она равна нулю.(^3x^-квадратный корень)
y'=(2cos x+^3x^-^3п^/3)'=(2cos x)'+(^3x^)'-(^3п^/3)=2(-sin x)+^3^-0=-2sin x+^3^Выясним в каких точках производная равна нулю.
-2sin x+^3^=02sin x=^3^sin x=^3^/2x=(-1)k arcsin^3^/2+пk,k принадлежит ZВ условиях задачи задан отрезок [0;п/2], поэтому нам нужно выбрать только значения из этого промежутка. Этому условию удовлетворяет только точка x=п/3.
Найдем значение функции в этой точке:
y(п/3)=2cos(п/3)+^3^*(п/3)-^3п^/3=2*1/2+^3п^/3-^3п^/3=1
Найдем значения функции на концах отрезка:
y(0)=2cos 0+^3^*0-^3п^/3=2-^3п/3^
y(п/2)=2cos(п/2)+^3^*п/2-^3п^/3=2*0+^3п^/2-^3п^/3=^3п^/6
Выбираем максимальное из трех значений 1,2 - ^3п^/3, ^3п^/6. Это 1.
ответ: 1