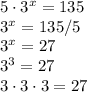
∫(х³/(4-х²)dx=?
Подынтегральное выражение можно представить в виде
х³/(4-х²)=(4х/(4-х²))-х,
Действительно, если почленно уголком разделим х³ на (4-х²), в частном будет -х, в остатке 4х, поэтому дробь х³/(4-х²)=(4х/(4-х²))-х, а интеграл тогда разобьется на два таких интеграла ∫((х³/(4-х²))dх= ∫(4х/(4-х²))dх +∫(-х)dх = -2∫(-2х)dх /(4-х²)-∫хdх =-2*∫ d(4-х²)/(4-х²)-∫х dх =-2㏑I(4-х²)I -x²/2+c, где с=const
ответ ∫(х³/(4-х²)dx=-2㏑I(4-х²)I -(x²/2)+c, где с=const
Промежутки знакопостоянства - это промежутки, где функция принимает значения одного знака, т.е. те промежутки из области определения функции, где значения функции положительны или отрицательны, т.е. у > 0 и y < 0. Поэтому решим неравенства f(x) > 0 и f(x) < 0.
Т.к. функция f(x) = 2x - 5 - линейная и пересекает ось Ох в одной точке, то:
2х - 5 > 0,
2х > 5,
х > 2,5, т.е. f(x) > 0 при х ∈ (2,5; +∞),
тогда f(x) < 0 при х ∈ (-∞; 2,5).
ответ: f(x) > 0 при х ∈ (2,5; +∞), f(x) < 0 при х ∈ (-∞; 2,5).
конечно:)
5*3^x=135
3^x=135/5
3^x=27
3^x=3^3
x=3