Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
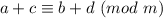
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
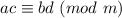
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
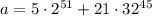
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,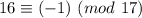 
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что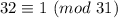 
, получаем
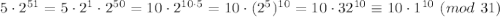
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
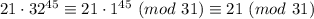
Остаток 21, чудесно. Выполняем последний шаг.
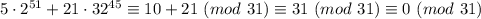
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
Для того, чтобы вычислить вероятность, сначала посмотрим на возможные исходы. Бросаем 2 монетки, значит могут быть следующие исходы:
1)на 1 монете выпадет ОРЕЛ, на второй ОРЕЛ
2)на 1 выпадет ОРЕЛ, на второй РЕШКА
3)на 1 выпадет РЕШКА, на второй ОРЕЛ
4)на 1 выпадет РЕШКА, на второй РЕШКА.
Больше исходов быть не может. Вспомнои формулу нахождения вероятности:
P=m/n, где m - благоприятные исходы, n - все исходы.
В нашем случае: Р=1 (потому что в перечисленных вышеискодах один раз выпадает два орла) / 4 (потому что мы посчитали, что исходов в даннной ситуации четыре)=0,25
ответ: 0,25
Если нам нужно сложить ПОСЛЕДОВАТЕЛЬНЫЕ числа то есть одна хитрая закономерность:
например 1+2+3+4++10 то нужно разбить числа на пары
1+10=11; 2+9=11; 3+8=11; 4*7=11; 5+6=11
Таких пар 5 (10/2=5) и каждая в сумме дает 11. Значит сумма всех чисел 11*5=55
Теперь рассмотрим наш пример
-1-2-3-4-5-6-7-8-9-10-11
Есть последовательность от -1 до -11
всего пар 11:2= 5 и остаток 1
Значит пар будет 5 и одно число(в центре) осталось без пары.
Какое же это число? Это число -6
Найдем сумму крайних чисел
-1+(-11)=-12
Значит сумма этих чисел равна
5*(-12)+(-6)=-60-6= -66