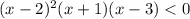
Имеем неравенство высокого порядка. Решим его методом интервалов.
1) Найдем точки пересечения функции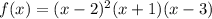 
с осью абсцисс, приравняв ее к нулю:
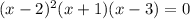
Произведение множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю:
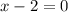, или 
, или 
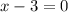
Тогда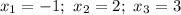 
— абсциссы точек пересечения функции 
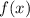с осью абсцисс.
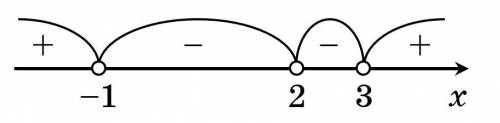
2) Выясним знак (значение) функции 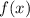на каждом из четырех участков, подставляя любое значение 
из заданного промежутка в функцию (см. вложение).
Следовательно, решением неравенства будет промежуток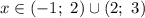 
ответ: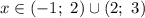
Объяснение:
Так как по формуле нахождения пути S=Vt => V=S/t (где S - расстояние, V - скорость, t - время пути)
Таким образом разделив расстояние между базами на время пути по течению реки, мы найдем скорость катера ПО течению реки: 48 км : 2 ч. = 24 км/ч.
Теперь нужно найти скорость катера ПРОТИВ течения реки. Для этого мы должны разделить расстояние на время плавание против течения: 48 км : 3 ч. = 16км/ч
Чтобы найти скорость катера, надо сначала узнать скорость течения реки. Для этого вычтем из скорости катера по течению скорость против течения и разделим результат на 2: (24 км/ч - 16 км/ч) : 2 = 4 км/ч
Теперь мы можем узнать скорость катера. Для этого мы из скорости катера ПО течению вычтем скорость течения: 24км/ч - 4км/ч = 20 км/ч
ответ: скорость катера - 20 км/ч, скорость течения - 4 км/ч
2sin²x-9sinx*cosx+7cos²x=0
Это однородное тригонометрическое уравнение второй степени.
cosx≠0
Разделим всё на cos²x
Получим:
2tg²x-9tgx+7=0
Пусть tgx=t, тогда
2t²-9t+7=0
D=(-9)²-4*2*7=81-56=25
t1=(9-5)/4=1
t2=(9+5)/4=14/4
Вернемся к замене
tgx=1 tgx=14/4
x=π/4+πk x=arctg14/4+πk