При яких значеннях а областю визначення функції у=√(x^2+aх+4) є всі дійсні числа?

👇

Ответ:

31Maks31

23.03.2022

$x^2+ax+4 \geq 0$
Знайдемо D
D=b^2-4ac=a^2-16

При D<0, нерівність буде мати розв'язок при всіх дійсних чисел
$a^2-16\ \textless \ 0\\ -4 \ \textless \ a \ \textless \ 4$

Відповідь: а ∈ (-4;4)

4,5(49 оценок)

Открыть все ответы

Ответ:

nnnnn777

23.03.2022

1. Выполним тождественное преобразование выражения и приведем его к виду квадратного уравнения:

(x - 1)(x + 4) = 0;

x² - 4x - x - 4 = 0;

x² - 5x - 4 = 0;

Выпишем коэффициенты:

старший коэффициент a = 1;

второй коэффициент b = - 5;

свободный член c = - 4.

2. Выполним тождественное преобразование выражения и приведем его к виду квадратного уравнения:

12 - 6(х - 3) - 7х = (х - 2)(х + 3);

12 - 6х + 18 - 7х = х² + 3х - 2х - 6;

- х² - 3х + 2х + 6 + 12 - 6х + 18 - 7х = 0;

- х² - 14х + 36 = 0;

х² + 14х - 36 = 0;

Выпишем коэффициенты:

старший коэффициент a = 1;

второй коэффициент b = 14;

свободный член c = - 36.

Объяснение:

4,4(76 оценок)

Ответ:

даун47

23.03.2022

Преобразуем левую часть:
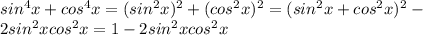
$sin^{4} x + cos^{4} x = ( sin^{2}x) ^{2} + (cos^{2}x) ^{2} = ( sin^{2}x + cos^{2}x) ^{2} - \\ 2 sin^{2} x cos^{2} x = 1 - 2 sin^{2} x cos^{2} x$

Далее:
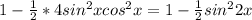
$1 - \frac{1}{2} * 4 sin^{2} x cos^{2}x = 1 - \frac{1}{2} sin^{2} 2x$
Таким образом, получаем уравнение:
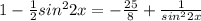
$1 - \frac{1}{2} sin^{2}2x = -\frac{25}{8} + \frac{1}{ sin^{2}2x }$
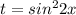Теперь понятно, что можно ввести замену $t = sin^{2}2x$ и продолжать решение уже дробно-рационального уравнения.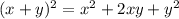

Советую запомнить приём, который я здесь употребил. Он состоит вот в чём.
Мы помним формулу сокращённого умножения:
$(x+y)^{2} = x^{2} + 2xy + y^{2}$
Отсюда я могу легко выразить сумму квадратов:
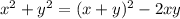
$x^{2} + y^{2} = (x+y)^{2} - 2xy$
Думаю, Вы уже догадались, что в нашем уравнении сыграло роль x, а что y.
Этот приём встречается очень часто в самых неожиданных ситуациях, так что рекомендую запомнить его.
Уравнение можно было решить и по формулам понижения степени(правда, это значительно было бы сложнее). Но в целом, можно рассмотреть и такой вариант, но я показал проще.

Делаем замену:
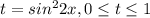
$t = sin^{2} 2x, 0 \leq t \leq 1$
После замены получаем:
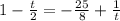
$1 - \frac{t}{2} = - \frac{25}{8} + \frac{1}{t}$
Умножаем обе части уравнения на 8t(с дробями работать крайне неудобно, да и t в знаменателе нам ни к чему - просто запомним, что он должен быть отличным от 0, а потом проверим это):
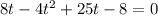
$8t - 4 t^{2} + 25t - 8 = 0$
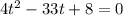
$4 t^{2} - 33t + 8 = 0$
Решаем квадратное уравнение(кстати, t уже отличен от 0. В этом можно убедиться прямой подстановкой)
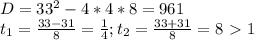$D = 33^{2} - 4 * 4 * 8 = 961 \\ 
 t_{1} = \frac{33 - 31}{8} = \frac{1}{4}; t_{2} = \frac{33 + 31}{8} = 8 \ \textgreater \ 1$ - этот корень не удовлетворяет нашему уравнению.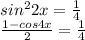
Следовательно, возвращаясь к переменной x, получаем простейшее уравнение:
$sin^{2} 2x = \frac{1}{4} \\ \frac{1 - cos 4x}{2} = \frac{1}{4}$
Отсюда
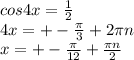
$cos 4x = \frac{1}{2} \\ 4x = +- \frac{ \pi }{3} + 2 \pi n \\ x = +- \frac{ \pi }{12} + \frac{ \pi n}{2}$
Это и есть ответ. Напомню, что при решении простейшего уравнения я использовал формулу понижения степени, а в конечном результате n - целое число.

4,7(25 оценок)

Это интересно:

Хобби-и-рукоделие

24.08.2021

Как сшить детское платье: пошаговая инструкция...

Питомцы-и-животные

06.11.2020

Как убить муху: 5 действенных способов...

Кулинария-и-гостеприимство

17.08.2020

Шоколадная водка: рецепты домашнего приготовления...

Стиль-и-уход-за-собой