1. у=8х-3
1). х=2: 8*2-3=13
2). 8х-3=19
8х=19+3
8х=22 |:8
х=2,75
3). В(-2;-13)
Подставляем: 8*(-2)-3=-19
-19≠-13
ответ: не проходит.
2. Смотри рисунок
1). у=1
2). х=3
3). -2х+5<0
-2х<-5 |:2
х>5/2
х>2,5
3. Приравниваем их:
47х-9=-13х+231
47х+13х=231+9
60х=240 |:60
х=4
Теперь считаем у: 47*4-9=179
(4;179)
5. у=-0,8х+4
С осью Ох (у=0): -0,8х+4=0
-0,8х=-4 |: (-0,8)
х=5
(5;0)
С осью Оу (х=0): -0,8*0+4=0+4=4
(0;4)
6. Чтобы две прямые были паралельны, нужно чтобы угловые коэффициенты были одинаковы. В данном случае это -5. y=-5x+b.
8=-5*(-2)+b, 8=10+b, b=-2, у=-5х-2.

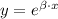 .
.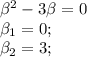
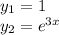
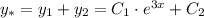
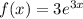
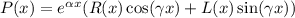 , где R(x) и S(x) - полиномы, которое имеет частное решение.
, где R(x) и S(x) - полиномы, которое имеет частное решение.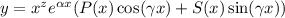 , где
, где 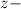 кратность корня
кратность корня 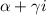
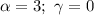
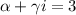 является корнем характеристического уравнения кратности z=1
является корнем характеристического уравнения кратности z=1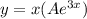
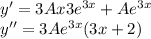
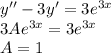
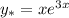
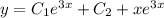
наименьшее такое двузначное -- первый член прогрессии находим (в виду небольшого делителя) достаточно легко перебором
10- наименьшее двузначное число
10:4=2(ост 2)
11:4=2(ост 3)
11 - первый член прогрессии
(либо оценивая по общей формуле с нахождения наименьшего(наибольшего) натурального удовлетворяющего неравенство
так как при делении на 4 остаток 3 общая форма 4k+3
4k+3>=10
4k>=10-3
4k>=7
4k>=7:4
k>=1.275
наименьшее натуральное k=2
при k=2: 4k+3=4*2+3=11
11 -первый член
)
далее
разность прогрессии равна числу на которое делим т.е. в данном случае 4
далее ищем последний член прогрессии
99- наибольшее двузначное
99:4=24(ост3)
значит 99 - последний член прогрессии
(либо с оценки неравенством
4l+3<=99
4l<=99-3
4l<=96
l<=96:4
l<=24
24 - Наибольшее натуральное удовлетворяющее неравенство
при l=24 : 4l+3=4*24+3=99
99- последний член прогрессии
)
далее определяем по формуле количество членов
и находим сумму по формуле
ответ: 1265