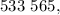 которая должна выражать дату (в каком-то неизвестном представлении).
которая должна выражать дату (в каком-то неизвестном представлении).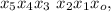


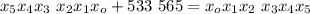 ;
;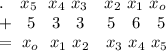

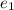 – возможная добавочная единица, уходящая из первого
– возможная добавочная единица, уходящая из первого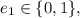
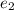 – возможная добавочная единица, уходящая из второго
– возможная добавочная единица, уходящая из второго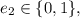
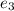 – возможная добавочная единица,
– возможная добавочная единица,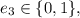
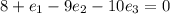 ;
;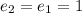 и при
и при  ;
;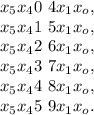
 поскольку
поскольку 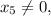 так как с этой цифры начинается разностное число.
так как с этой цифры начинается разностное число. поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.
поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.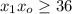 .
.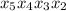 .
.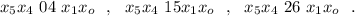
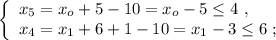

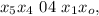
 может играть роль апреля.
может играть роль апреля.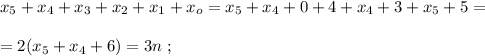
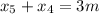 ;
;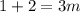 ;
;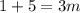 ;
;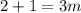 ;
; ;
;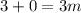 ;
;
 – дата 12/04/56 г.
– дата 12/04/56 г. – дата 15/04/86 г.
– дата 15/04/86 г.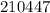 – дата 21/04/47 г.
– дата 21/04/47 г.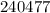 – дата 24/04/77 г.
– дата 24/04/77 г.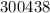 – дата 24/04/38 г.
– дата 24/04/38 г.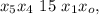
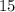 может играть только роль числа месяца (дня).
может играть только роль числа месяца (дня).
 ;
;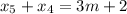 ;
;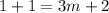 ;
;
 – дата 11/15/46 г.
– дата 11/15/46 г.

g=3,−13g=3,-13
Десятичный вид:
g=3,−0.¯3
Объяснение:
Упростим каждый член.
Нажмите, чтобы увидеть больше шагов...
5g−6(2g+3)(2g−3)−3(1−g)3+2g=32g−35g-6(2g+3)(2g-3)-3(1-g)3+2g=32g-3
Изменим порядок членов.
5g−6(2g+3)(2g−3)−3(1−g)2g+3=32g−35g-6(2g+3)(2g-3)-3(1-g)2g+3=32g-3
Для записи −3(1−g)2g+3-3(1-g)2g+3 в виде дроби с общим знаменателем, умножим ее на 2g−32g−32g-32g-3.
5g−6(2g+3)(2g−3)−3(1−g)2g+3⋅2g−32g−3=32g−35g-6(2g+3)(2g-3)-3(1-g)2g+3⋅2g-32g-3=32g-3
Упростим члены.
5g−6−3(1−g)(2g−3)(2g+3)(2g−3)=32g−35g-6-3(1-g)(2g-3)(2g+3)(2g-3)=32g-3
Упростим числитель.
6g2−10g+3(2g+3)(2g−3)=32g−36g2-10g+3(2g+3)(2g-3)=32g-3
Найдем НОЗ членов уравнения.
(2g+3)(2g−3)(2g+3)(2g-3)
Умножим каждый член на (2g+3)(2g−3)(2g+3)(2g-3) и упростим.
6g2−10g+3=6g+96g2-10g+3=6g+9
Решим уравнение.
g=3,−13g=3,-13
Результат можно выразить в различном виде.
Точная форма:
g=3,−13g=3,-13
Десятичный вид:
g=3,−0.¯3
210*(х-4)+210*(х+4)\(х+4)*(х-4)=18
Раскроем скобки и приведем подобные в числителе
210х-840+840+210х+840\(х+4)*(х-4)=18
Дальше свернем з6
анаменатель в разность квадратов) и перемножим крест накрест как в пропорции
420х=18*(х^2-16)
разделим обе части уравнения на 6
70х=3(х^2-16)
раскроем скобки
70[=3x^2-48
3x^2-70x-48=0
решаем квадратное уравнение
D=4900+576=5476=74^2
x1=-2\3
x2=24