1)cos t=1/2
t=±p/3+2pk kEZ
2)ctg(-t)*sint + cos(p+t)=cost/-sint *sint - cost=-2cost
3)tgt*cost=(tgt + ctgt)^-1
sint/cost * cost =1 / sint/cost + cost/sint
sint=1 / (sin^2t+cos^2t)/sint*cost
sint=sint*cost / 1
sint=sint*cost
тождества не верны
4) 4sin 690 - 8cos^210+ √27*ctg660=4sin(360+180+90+60) - 8cos (180+30) +
+ √27 * sin(360+180+90+30) /cos(360+180+90+30)=4*(-1/2) - 8*(-√3 /2) +
+ 3√3*(-√3 /2) : 1/2=-2+4√3- 9=7+4√3
5) Дано: cost=-3/5., пи/2<t<пи => II четверть
sint=±√1-cos^2t= ±√1-9/25= ±4/5
sint=4/5 тк он во II четверти
tgt=4/5 : (-3/5)=-4/3
ctgt=-3/4
6) sin(10,52) - tg(10,5) - cos (10,5) - ctg(10,5)
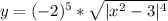
Т.к. модуль возводиться в чётную степень, от него можно избиваться.
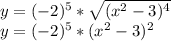
1. Область определения все числа.
2. От х берётся чётная степень, поэтому функция чётная (со словами просто совпадение), то есть y(x)=y(-x), таким образом можно построить график функции справа и отразить его на лево.
3. Найдём точки пересечения с осями:
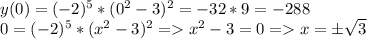
4. Исследование с первой производной (экстремумы и возрастания и убывание функции).
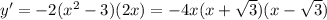
Cм. внизу
5. Исследование с второй производной (точки перегиба, выпуклости и вогнутости).
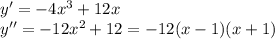
См. внизу
6. Исследование на асимптоты:
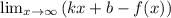
Формула чтобы найти уравнение асимптоты. Найдём k.
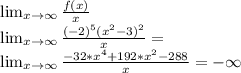
Т.к. коэффициент равен -∞, то асимптот не существует.
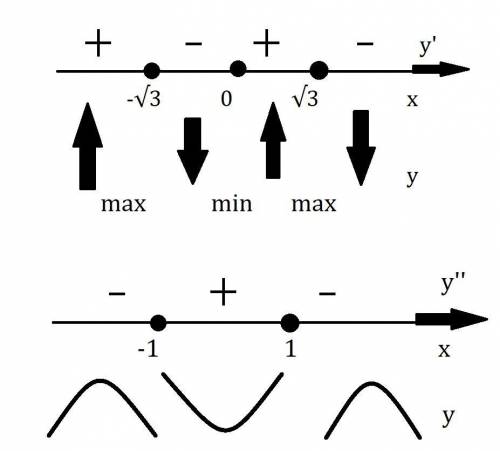
разделим 244 на эту сумму
160*3/4=120
160*2/5=64
160*3/8=60