Объяснение:
если известно, что искомая прямая y₁ = k₁x +b₁ параллельна прямой y=-4x+51 (у=кх +b), то мы знаем коэффициент k₁ = -4 при x, т.к. у параллельных прямых коэффициенты k и к₁ при х равны.
тогда мы уже имеем "половину" уравнения у₁ = -4х +b₁
теперь для определения b₁ используем то, что искомая прямая проходит через точку M(-1; 3). это означает, что координаты точки должны удовлетворять уравнению у₁ = -4х +b₁. подставим эти координаты
3= -4*(-1) +b₁ тогда b₁ = -1
и искомое уравнение
у₁ = -4х -1
теперь проверим, принадлежит ли построенному графику точка N(-50; 200). подставим ее координаты в уравнение у₁ = -4х -1
200 ≠ -4*(-50)-1
точка N(-50; 200) ∉ графику функции у₁ = -4х -1
тогда строим график по двум точкам
х = -1 у₁(-1) = 3 точка M(-1; 3)
х = 0 у₁(0) = -1
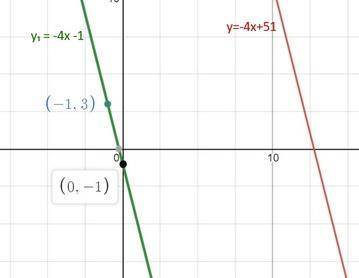
на первом фото построение по двум точкам у₁ = -4х -1 ║y=-4x+51
на втором показано, что точка N(-50; 200). ∉ графику у₁ = -4х -1

1.Поупражняемся вот в этой формуле ㏒ₐⁿсˣ=(х/n)㏒ₐс, конечно, при этом а больше нуля; а≠1, и с больше нуля,
㏒₍₅¹/²₎25/(√3+√14))¹=(1:(1/2))㏒₅(25/(√3+√14))=2㏒₅(25/(√3+√14))=
㏒₅(25/(√3+√14))²=㏒₅(625/(3+2√42+14)=㏒₅(625/(3+2√42+14)=
㏒₅(625/(17+2√42).
2. Рассмотрим детальнее второе слагаемое. но прежде 0.2=2/10=1/5=5⁻¹;
㏒₀,₂(1/(17+2√42)=㏒₍₅⁻¹₎17+2√42)¹=(1:(-1))㏒₅(1/(17+2√42)=-1*㏒₅(1/(17+2√42)=
㏒₅(1/(17+2√42)⁻¹=㏒₅(1:(1/(17+2√42))=㏒₅((17+2√42))
3. Вспомним свойство- сумма логарифмов с одинаковыми основаниями на области определения может быть заменена на логарифм произведения с тем же основанием. т.е.
㏒ₐс+㏒ₐb=㏒ₐ(сb)
㏒₅(625/(3+2√42+14)+㏒₅((17+2√42))=
㏒₅(625*(17+2√42)/(17+2√42))=㏒₅(625)=㏒₅(5)⁴=4*㏒₅(5)=4*1=4
log(2)25+log(5)p-log(5)S=2+3-4=1
2
log(7)a-log(7)49-log(7)b=2-2+1=1
3
log(11)m-log(11)11-log(11)n=4-1-2=1