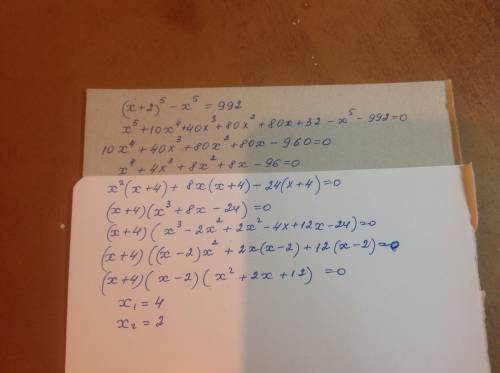


1)Найдите девятый член последовательности
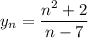

2) Найдите пятый член последовательности заданной рекуррентным у1 = ½, yₙ=2*y₍ₙ₋₁₎
y₂=2*1/2=1; y₃=2*1=2; y₄=2*2=4; y₅=2*4=8
3) Подберите формулу n- го члена последовательности - 2/2; 4/5; - 6/8; 8/11; -10/14;

проверка:
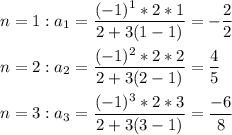
4) Сколько членов последовательности 3, 6, 9, 12,….меньше числа 95
аₙ=а₁+3(n-1)
aₙ<95
a₁+3(n-1)<95
3+3n-3<95
3n<95
n<31.(6)
n=31
проверим: a₃₁=3+3(31-1)=3+3*30=93
Значит 31 член меньше 95
5) у₁ = 2, у₂ = 1, уₙ = 2y₍ₙ₋₂₎+3y₍ₙ₋₁₎ (n = 3,4,5,…).Найдите n, если известно, что уₙ = 83.
тут можно просто решить находя слены этой последовательности
y₁=2
y₂=1
y₃=2*2+3*1=4+3=7
y₄=2*1+3*7=2+21=23
y₅=2*7+3*23=14+69=83
N=5
3.
y = -x^2 + 4x + 5
Решаем через дискриминант.
D = b^2 - 4ac = 16 - 4 * (-1) * 5 = 16 + 20 = 36
x1 = (-b - sqrt(D)) / 2a = (- 4 - 6) / 2 = -5
x2 = (-b + sqrt(D)) / 2a = (- 4 + 6) / 2 = 1
Проверка: 25 - 20 + 5 = 1 + 4 + 5 = 10.
4.
x - y = 3
x^2 - xy - 2y^2 = 7
Здесь можно выразить х через у, используя первое выражение.
х = у + 3
Подставляем его во второе выражение:
(y + 3)^2 - (y + 3) * y - 2y^2 = 7
(y + 3)^2 = y^2 + 6y + 9 - по формуле сокращенного умножения
(y + 3) * y = y^2 + 3y
y^2 + 6y + 9 - y^2 - 3y - 2y^2 = 7
3y + 9 - 2y^2 = 7
-2y^2 + 3y + 9 = 7 - приводим к нулю
-2y^2 + 3y + 2 = 0 - теперь у нас квадратичное уравнение, решаем как всегда.
D = b^2 - 4ac = 9 - (-16) = 25
y1 = (-b - sqrt(D)) / 2a = (-3 - 5) / -4 = 2
y2 = (-b + sqrt(D)) / 2a = (-3 + 5) / -4 = -0,5
Подставляем к значениям х:
х1 - 2 = 3
x1 = 5
Проверяем по второму выражению:
25 - 10 - 8 = 7
x2 - (-0,5) = 3
x2 = 2,5
Проверяем по второму выражению:
6.25 + 1.25 - 0.5 = 7
В обоих случаях все сошлось.
ответ: х1 = 5, у1 = 2; х2 = 2,5, у2 = -0,5.