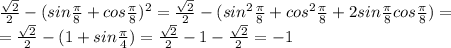Подставим х=8, у=0 в выражение у=ах²+bx+c получим 0=а·8²+b·8+c 64a+8b+c=0
Наименьшее значение в вершине параболы, при условии, что ветви параболы направлены вверх, при этом а > 0 абсцисса вершины: х₀=-b/2а ⇒ 6=-b/2a ⇒-b=12a ⇒ b=-12a y₀=a·6²+b·6+c ⇒ -12=36a+6b+c Решаем систему трех уравнений с тремя неизвестными: { 64a+8b+c=0 ⇒ 64 a + 8· (-12a)+c=0 -32a + c= 0 (*) { b=- 12a { -12=36a+6b+c ⇒ 36a +6·(-12a)+c=-12 -36a +c= -12 (**)
1) 2sinП/8*cosП/8 - это формула двойного угла
2)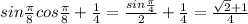
3) cos^2*П/8-sin^2*П/8 - это формула двойного угла
4)