5050
Объяснение:
Карл Фридрих Гаусс заметил интересную закономерность, что если сгруппировать числа в пары получается алгоритм , благодаря которому можно быстро сложить числа от 1 до 100 .
Рассмотрим этот алгоритм :
1) Необходимо найти количество пар в ряду натуральных чисел. В нашем ряду 100 чисел , значит количество пар будет :
100 : 2 = 50 пар
2) Необходимо сложить первое и последнее число в ряду , в нашем случае это :
100 + 1 =101
3) Умножить сумму первого и последнего чисел в ряду на количество пар в ряду :
101 * 50= 5050
Получаем , что сумма чисел от 1 до 100 будет 5050
Сегодня этот алгоритм называется - правило Гаусса и широко применяется при устном счете
ОДЗ :
x² - 15 > 0
(x - √15)(x + √15) > 0
+ - +
__________₀______________₀__________
- √15 √15
/////////////////////// ////////////////////////
x ∈ (- ∞ ; - √15) ∪ (√15 ; + ∞)
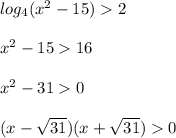
+ - +
____________₀___________₀___________
- √31 √31
////////////////////////// /////////////////////
ответ : x ∈ (- ∞ ; - √31) ∪ (√31 ; + ∞)
обозначим х²-3=у
у²+у-2=0
D=1+8=9 √D=⁺₋3
у₁=(-1+3)/2=1 у₂=(-1-3)/2=-2
х²-3=1
х²=4 х₁=2 х₂=-2
х²-3=-2
х²=1 х₃=1 х₄=-1
2х⁴-х³=0
х³(2х-1)=0
х₁=0
2х₂-1=0 х₂=0,5