Пусть первый пешеход движется со скоростью x км/ч, а второй - y км/ч.
В первом случае первый пешеход будет двигаться до встречи 4,5 ч , в то время как второй 2,5 ч (так как он вышел на два часа раньше второго). Из этого получаем уравнение: 4,5x+2,5y=30
Во втором случае второй пешеход шел 5 ч, а первый пешеход шел 5-2=3ч. Получаем второе уравнение: 3x+5y=30
Из этих двух уравнений составляем систему

Умножеим первое уравнение системы на 2:
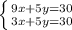
Вычтем из первого уравнения второе, получим:
6x=30
x=30:6
x=5.
Подставляя во второе уравнение, находим
3*5+5y=30
15+5y=30
5y=15
y=3
ответ: скорость первого - 5 км/ч, скорость второго - 3 км/ч.
докажем сначала пункт б)
каждое натуральное число можна записать в виде 6k+1,6k+2, 6k+3, 6k+4, 6k+5, (то же самое что 6l-1), 6k+6, где k=0, или k - натуральное (так как при делении на 6 остатки могут быть 0,1,2,3,4,5)
числа вида 6k+2, 6k+4, 6k+6 четные поэтому делятся на 2, но но одно простое число больше 3 на 2 не делится, поэтому среди чисел этого вида нет простых
числа вида 6k+3=3*(2k+1) делятся на 3, но ни одно число большее 3, на 3 не делится, поэтому среди чисел данного вида нет протых чисел, поэтому простые числа находятся срди чисел вида р=6к+-1, к принадлежит N, что и требовалось доказать
теперь используя доказанный пункт б) докажем а)
р*р-1=(p-1)(p+1) - по формуле разности квадратов
рассмотрим два возможных случая
первый р=6k+1, к принадлежит N
тогда
р*р-1=(6k+1-1)(6k+1+1)=6k*(6k+2)=12k*(3k+1), а значит деится на 12
второй p=6k-1
p*p-1=(6k-1-1)(6k-1+1)=(6k-2)*6к=12к*(3к-1), а значит делится на 12.
Доказано
sin(pi/4)*(-tg(pi/3))+cos(pi/6)=sqrt2/2*sqrt3+sqrt3/2=(sqrt6+sqrt3)/2