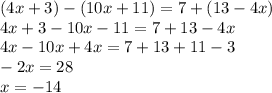
Вертикальные асимптоты: x = 2
Горизонтальные асимптоты: y = 3
Нет наклонных асимптот
Объяснение:
Выясним, при каких значениях переменной функция 3 x + 1 x − 2 не определена. x = 2
Рассмотрим рациональную функцию
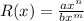, где n - степень числителя, а m - степень знаменателя.
1. Если n < m , то ось x, y = 0 , является горизонтальной асимптотой.
2. Если n = m , то горизонтальной асимптотой является прямая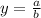 
Если n > m , то не существует горизонтальной асимптоты (только наклонная асимптота).
Найдем n и m
n = 1 ; m = 1
Поскольку n = m , горизонтальная асимптота является прямой 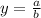, где a = 3 и b = 1
y = 3
Наклонных асимптот нет, поскольку степень числителя меньше либо равна степени знаменателя.
Это множество всех асимптот.
Вертикальные асимптоты: x = 2
Горизонтальные асимптоты: y = 3
Нет наклонных асимптот
4х-10х+4х=7+13-3+11
-2х=28
х=-14